如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)
问题背景:如图1,等腰 中, , ,作 于点 ,则 为 的中点, ,于是 ;
迁移应用:如图2, 和 都是等腰三角形, , , , 三点在同一条直线上,连接 .
①求证: ;
②请直接写出线段 , , 之间的等量关系式;
拓展延伸:如图3,在菱形 中, ,在 内作射线 ,作点 关于 的对称点 ,连接 并延长交 于点 ,连接 , .
①证明 是等边三角形;
②若 , ,求 的长.

如图,平面直角坐标系中O为坐标原点,直线y= x+6与x轴、y轴分别交于A、B两点,C为OA中点;
x+6与x轴、y轴分别交于A、B两点,C为OA中点;
(1)求直线BC解析式;
(2)动点P从O出发以每秒2个单位长度的速度沿线段OA向终点A运动,同时动点Q从C出发沿线段CB以每秒 个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t(s),求y于t的函数关系式;
个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t(s),求y于t的函数关系式;
(3)在(2)的条件下,以PC为直径作⊙N,求t为何值时直线QM与⊙N相切.
温岭是受台风影响较为严重的城市之一.如图,坡上有一颗与水平面EF垂直的大树AB,台风过后,大树倾斜后折断倒在山坡上,大树顶部B接触到坡面上的D点.已知山坡的坡角∠AEF=30°,量得树干倾斜角∠BAC=45°,大树被折断部分和坡面所成的角∠ADC=60°且AD=4米.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度AB.(结果精确到个位,参考数据: ≈1.4,
≈1.4, ≈1.7,
≈1.7, ≈2.4)
≈2.4)
如图,在 中, ,以斜边 上的中线 为直径作 ,与 交于点 ,与 的另一个交点为 ,过 作 ,垂足为 .
(1)求证: 是 的切线;
(2)若 的直径为5, ,求 的长.

如图,在矩形 中, , ,点 是 边上的点, ,连接 , 交于点 .
(1)求证: ;
(2)连接 ,求 的值;
(3)连接 交 于点 ,求 的值.

如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,tan A=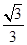 ,AD=20.求BC的长.
,AD=20.求BC的长.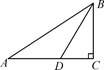
如图,已知 是 的直径,过 点作 ,交弦 于点 ,交 于点 ,且使 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

如图,在Rt△ABC中,∠ACB=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长DE交BC的延长线于点F.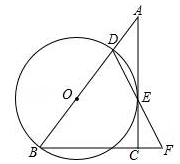
(1)求证:BD=BF;
(2)若CF=1,cosB=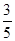 ,求⊙O的半径.
,求⊙O的半径.
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB= ,AD=1.
,AD=1.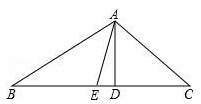
(1)求BC的长;
(2)求tan∠DAE的值.
如图,在正方形 中,点 在对角线 上(不与点 , 重合), 于点 , 于点 ,连接 .
(1)写出线段 , , 长度之间的数量关系,并说明理由;
(2)若正方形 的边长为1, ,求线段 的长.

如图, 已知四边形 是菱形, 于点 , 于点 .
(1) 求证: ;
(2) 若 , ,求 的值 .

如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120m.试求大楼AB的高度(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,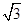 ≈1.73)
≈1.73)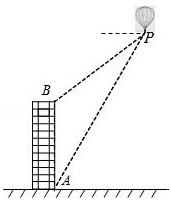
如图,AB是⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.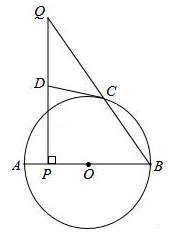
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由;
(2)若cosB=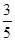 ,AP=1,求QC的长.
,AP=1,求QC的长.