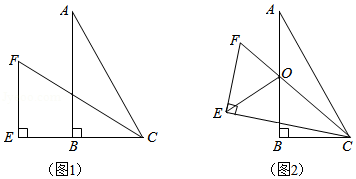
如图,已知AB是⊙O的直径,过点A作⊙O的切线MA,P为直线MA上一动点,以点P为圆心,PA为半径作⊙P,交⊙O于点C,连接PC、OP、BC.
(1)知识探究(如图1):
①判断直线PC与⊙O的位置关系,请证明你的结论;
②判断直线OP与BC的位置关系,请证明你的结论.
(2)知识运用(如图2):当PA>OA时,直线PC交AB的延长线于点D,若BD=2AB,求tan∠ABC的值.
如图①,南京中山陵的台阶拾级而上被分成坡度不等的两部分.图②是台阶的侧面图,若斜坡BC长为120m,在C处看B处的仰角为25°;斜坡AB长70m,在A处看B处的俯角为50°,试求出陵墓的垂直高度AE的长.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47)
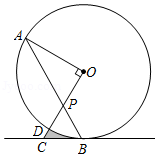
如图,是
的弦,
是
外一点,
,
交
于点
,交
于点
,且
.
(1)判断直线与
的位置关系,并说明理由;
(2)若,
,求图中阴影部分的面积.
如图1,与直线
相离,过圆心
作直线
的垂线,垂足为
,且交
于
、
两点
在
、
之间).我们把点
称为
关于直线
的“远点“,把
的值称为
关于直线
的“特征数”.
(1)如图2,在平面直角坐标系中,点
的坐标为
.半径为1的
与两坐标轴交于点
、
、
、
.
①过点画垂直于
轴的直线
,则
关于直线
的“远点”是点 (填“
”.“
”、“
”或“
”
,
关于直线
的“特征数”为 ;
②若直线的函数表达式为
.求
关于直线
的“特征数”;
(2)在平面直角坐标系中,直线
经过点
,点
是坐标平面内一点,以
为圆心,
为半径作
.若
与直线
相离,点
是
关于直线
的“远点”.且
关于直线
的“特征数”是
,求直线
的函数表达式.

如图1,点在线段
上,
,
,
,
.
(1)点到直线
的距离是 ;
(2)固定,将
绕点
按顺时针方向旋转
,使得
与
重合,并停止旋转.
①请你在图1中用直尺和圆规画出线段经旋转运动所形成的平面图形(用阴影表示,保留画图痕迹,不要求写画法).该图形的面积为 ;
②如图2,在旋转过程中,线段与
交于点
,当
时,求
的长.
如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
(1)求证:CF为⊙O的切线;
(2)若⊙O的半径为 cm,弦BD的长为3cm,求CF的长.
cm,弦BD的长为3cm,求CF的长.
在矩形中,
为
边上一点,把
沿
翻折,使点
恰好落在
边上的点
.
(1)求证:;
(2)若,
,求
的长;
(3)若,记
,
,求
的值.

如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,tan A=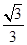 ,AD=20.求BC的长.
,AD=20.求BC的长.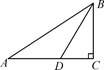
如图,已知 是 的直径,过 点作 ,交弦 于点 ,交 于点 ,且使 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

如图,在Rt△ABC中,∠ACB=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长DE交BC的延长线于点F.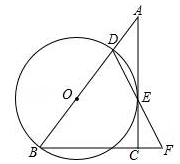
(1)求证:BD=BF;
(2)若CF=1,cosB=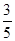 ,求⊙O的半径.
,求⊙O的半径.
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB= ,AD=1.
,AD=1.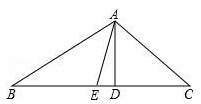
(1)求BC的长;
(2)求tan∠DAE的值.
如图,在正方形 中,点 在对角线 上(不与点 , 重合), 于点 , 于点 ,连接 .
(1)写出线段 , , 长度之间的数量关系,并说明理由;
(2)若正方形 的边长为1, ,求线段 的长.

如图, 已知四边形 是菱形, 于点 , 于点 .
(1) 求证: ;
(2) 若 , ,求 的值 .

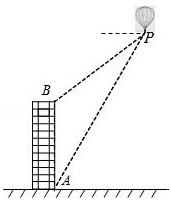
如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120m.试求大楼AB的高度(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,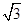 ≈1.73)
≈1.73)