江苏省常州市武进区中考一模数学试卷
已知一粒大米的质量约为0.000021千克,这个数用科学记数法表示为( )
| A.0.21×10﹣4 | B.2.1×10﹣4 | C.0.21×10﹣5 | D.2.1×10﹣5 |
)如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是( )
| A.主视图的面积为5 |
| B.左视图的面积为3 |
| C.俯视图的面积为3 |
| D.三种视图的面积都是4 |
若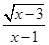 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
| A.x≥3 | B.x≤3且x≠1 | C.1<x≤3 | D.x≥1且x≠3 |
如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )
A. |
B. |
C. |
D. |
如图,将矩形纸片的两只直角分别沿EF、DF翻折,点B恰好落在AD边上的点B′处,点C恰好落在边B′F上.若AE=3,BE=5,则FC= .
如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线 相切,设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当r1=1时,r2015= .
相切,设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当r1=1时,r2015= .
某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
| 组别 |
正确字数x |
人数 |
| A |
0≤x<8 |
10 |
| B |
8≤x<16 |
15 |
| C |
16≤x<24 |
25 |
| D |
24≤x<32 |
m |
| E |
32≤x<40 |
n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
小明在学习反比例函数的图象时,他的老师要求同学们根据“探索一次函数y1=x+1的图象”的基本步骤,在纸上逐步探索函数y2= 的图象,并且在黑板上写出4个点的坐标:A(
的图象,并且在黑板上写出4个点的坐标:A( ,
, ),B(1,2),C(1,
),B(1,2),C(1, ),D(﹣2,﹣1).
),D(﹣2,﹣1).
(1)在A、B、C、D四个点中,任取一个点,这个点既在直线y1=x+1又在双曲线y2= 上的概率是多少?
上的概率是多少?
(2)小明从A、B、C、D四个点中任取两个点进行描点,求两点都落在双曲线y2= 上的概率.
上的概率.
如图,矩形ABCD中,点E,F分别在AB,CD边上,连接CE、AF,∠DCE=∠BAF.试判断四边形AECF的形状并加以证明.
如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
如图,每个网格都是边长为1个单位的小正方形,△ABC的每个顶点都在网格的格点上,且∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以点A为旋转中心,按顺时针方向旋转90°后得到的图形△AB1C1;
(2)试在图中建立直角坐标系,使x轴∥AC,且点B的坐标为(﹣3,5);
(3)在(1)与(2)的基础上,若点P、Q是x轴上两点(点P在点Q左侧),PQ长为2个单位,则当点P的坐标为 时,AP+PQ+QB1最小,最小值是 个单位.
一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:
| 销售单价x(元) |
50 |
60 |
70 |
80 |
| 年销售量y(万件) |
5.5 |
5 |
4.5 |
4 |
(1)求y关于x的函数关系式;
(2)写出该公司销售这种产品的年利润w(万元)关于销售单价x(元)的函数关系式;当销售单价x为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象帮助该公司确定产品的销售单价范围,使年利润不低于60万元.
已知△ABC中,∠C是其最小的内角,如果过顶点B的一条直线把这个三角形分割成了两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为△ABC的关于点B的伴侣分割线.例如:如图1,在Rt△ABC中,∠C=20°,过顶点B的一条直线BD交AC于点D,且∠DBC=20°,显然直线BD是△ABC的关于点B的伴侣分割线.
(1)如图2,在△ABC中,∠C=20°,∠ABC=110°.请在图中画出△ABC的关于点B的伴侣分割线,并标注角度;
(2)在△ABC中,设∠B的度数为y,最小内角∠C的度数为x.试探索y与x之间满足怎样的关系时,△ABC存在关于点B的伴侣分割线.
如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F.设DF=x,EC=y.
(1)求y关于x的函数关系式,并写出x的取值范围.
(2)当CF=1时,求EC的长.
(3)若直线AF与线段BC延长线交于点G,当△DBE与△DFG相似时,求DF的长.





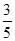 ,则∠C的正弦值等于( )
,则∠C的正弦值等于( )



 = ,(﹣2015)0= ,(2﹣1)2= .
= ,(﹣2015)0= ,(2﹣1)2= . 上,点Q(﹣a,2b)在直线y=x+1上,则代数式a2﹣4b2﹣1= .
上,点Q(﹣a,2b)在直线y=x+1上,则代数式a2﹣4b2﹣1= .
 .
.
 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号