初中数学解直角三角形解答题

如图，海上 $B、C$两岛分别位于 $A$岛的正东和正北方向，一艘船从 $A$岛出发，以18海里/时的速度向正北方向航行2小时到达 $C$岛,此时测得 $B$岛在 $C$岛的南偏东 $43°$，求 $A、B$两岛之间的距离．（结果精确到0．1海里）
【参考数据：】

如图所示：与的边相切于点，与、分别交于点、，．是的直径．连接，过作交于，连接、，与交于点．

（1）求证：直线与相切；

（2）求证：；

（3）若，时，过作交于、两点在线段上），求的长．

【发现】如图①，已知等边 $\mathit{\Delta ABC}$，将直角三角板的 $60°$角顶点 $D$任意放在 $\mathit{BC}$边上（点 $D$不与点 $B$、 $C$重合），使两边分别交线段 $\mathit{AB}$、 $\mathit{AC}$于点 $E$、 $F$．

（1）若 $\mathit{AB}=6$， $\mathit{AE}=4$， $\mathit{BD}=2$，则 $\mathit{CF}=$　　；

（2）求证： $\mathit{\Delta EBD}\backsim \mathit{\Delta DCF}$．

【思考】若将图①中的三角板的顶点 $D$在 $\mathit{BC}$边上移动，保持三角板与边 $\mathit{AB}$、 $\mathit{AC}$的两个交点 $E$、 $F$都存在，连接 $\mathit{EF}$，如图②所示，问：点 $D$是否存在某一位置，使 $\mathit{ED}$平分 $\angle \mathit{BEF}$且 $\mathit{FD}$平分 $\angle \mathit{CFE}$？若存在，求出 $\frac{\mathit{BD}}{\mathit{BC}}$的值；若不存在，请说明理由．

【探索】如图③，在等腰 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$，点 $O$为 $\mathit{BC}$边的中点，将三角形透明纸板的一个顶点放在点 $O$处（其中 $\angle \mathit{MON}=\angle B)$，使两条边分别交边 $\mathit{AB}$、 $\mathit{AC}$于点 $E$、 $F$（点 $E$、 $F$均不与 $\mathit{\Delta ABC}$的顶点重合），连接 $\mathit{EF}$．设 $\angle B=\alpha$，则 $\mathit{\Delta AEF}$与 $\mathit{\Delta ABC}$的周长之比为　　（用含 $\alpha$的表达式表示）．

如图，在Rt△ABC中，∠C＝90°，BD平分∠ABC，tan A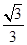＝，AD＝20．求BC的长．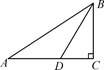

莘县旅游资源丰富，其中燕塔是莘县著名旅游景点（如图①）．一天身高1．5m的小明从A处仰视观看燕塔顶部，其仰角为30°．小明又向西走了30m，∠APB=15°（如图②）．请你帮小明算出雁塔的高度．（结果保留一位小数，参考数据：≈1．41，≈1．73）

如图，已知 $\mathit{AB}$是 $\odot O$的直径，过 $O$点作 $\mathit{OP}\perp \mathit{AB}$，交弦 $\mathit{AC}$于点 $D$，交 $\odot O$于点 $E$，且使 $\angle \mathit{PCA}=\angle \mathit{ABC}$．

（1）求证： $\mathit{PC}$是 $\odot O$的切线；

（2）若 $\angle P=60°$， $\mathit{PC}=2$，求 $\mathit{PE}$的长．

如图，在Rt△ABC中，∠ACB=90°，点D是AB边上一点，以BD为直径的⊙O与边AC相切于点E，连接DE并延长DE交BC的延长线于点F．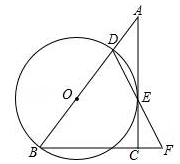

（1）求证：BD=BF；
（2）若CF=1，cosB=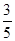，求⊙O的半径．

如图，在△ABC中，AD是BC边上的高，AE是BC边上的中线，∠C=45°，sinB=，AD=1．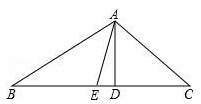

（1）求BC的长；
（2）求tan∠DAE的值．

如图，在正方形 $\mathit{ABCD}$中，点 $G$在对角线 $\mathit{BD}$上（不与点 $B$， $D$重合）， $\mathit{GE}\perp \mathit{DC}$于点 $E$， $\mathit{GF}\perp \mathit{BC}$于点 $F$，连接 $\mathit{AG}$．

（1）写出线段 $\mathit{AG}$， $\mathit{GE}$， $\mathit{GF}$长度之间的数量关系，并说明理由；

（2）若正方形 $\mathit{ABCD}$的边长为1， $\angle \mathit{AGF}=105°$，求线段 $\mathit{BG}$的长．

如图， 已知四边形 $\mathit{ABCD}$是菱形， $\mathit{DF}\perp \mathit{AB}$于点 $F$， $\mathit{BE}\perp \mathit{CD}$于点 $E$．

（1） 求证： $\mathit{AF}=\mathit{CE}$；

（2） 若 $\mathit{DE}=2$， $\mathit{BE}=4$，求 $\sin \angle \mathit{DAF}$的值 ．

如图，利用热气球探测器测量大楼AB的高度．从热气球P处测得大楼顶部B的俯角为37°，大楼底部A的俯角为60°，此时热气球P离地面的高度为120m．试求大楼AB的高度（精确到0．1m）．（参考数据：sin37°≈0．60，cos37°≈0．80，tan37°≈0．75，≈1．73）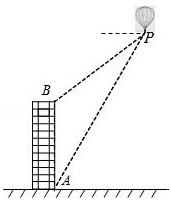

如图，AB是⊙O的直径，点C在⊙O上，点P是直径AB上的一点（不与A，B重合），过点P作AB的垂线交BC的延长线于点Q．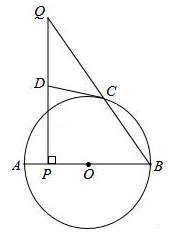

（1）在线段PQ上取一点D，使DQ=DC，连接DC，试判断CD与⊙O的位置关系，并说明理由；
（2）若cosB=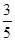，AP=1，求QC的长．

如图， $\mathit{CE}$是 $\odot O$的直径， $\mathit{BC}$切 $\odot O$于点 $C$，连接 $\mathit{OB}$，作 $\mathit{ED}//\mathit{OB}$交 $\odot O$于点 $D$， $\mathit{BD}$的延长线与 $\mathit{CE}$的延长线交于点 $A$．

（1）求证： $\mathit{AB}$是 $\odot O$的切线；

（2）若 $\odot O$的半径为1， $\tan \angle \mathit{DEO}=\sqrt{2}$，求 $\mathit{AE}$的长．

如图，一艘货轮在A处发现其北偏东45°方向有一海盗船，立即向位于正东方向B处的海警舰发出求救信号，并向海警舰靠拢，海警舰立即沿正西方向对货轮实施救援，此时距货轮200海里，并测得海盗船位于海警舰北偏西60°方向的C处．

（1）求海盗船所在C处距货轮航线AB的距离．
（2）若货轮以45海里/时的速度在A处沿正东方向海警舰靠拢，海盗以50海里/时的速度由C处沿正南方向对货轮进行拦截，问海警舰的速度应为多少时才能抢在海盗之前去救货轮？（结果保留根号）

如图，小丽假期在娱乐场游玩时，想要利用所学的数学知识测量某个娱乐场地所在山坡AE的高度．她先在山脚下的点E处测得山顶A的仰角是30°，然后，她沿着坡度i=1∶1的斜坡步行15分钟到达C处，此时，测得点A的俯角是15°．已知小丽的步行速度是18米/分，图中点A、B、E、D、C在同一平面内，且点D、E、B在同一水平直线上，求出娱乐场地所在山坡AE的高度AB．（精确到0．1米，参考数据：≈1．41）．