如图,一艘货轮在A处发现其北偏东45°方向有一海盗船,立即向位于正东方向B处的海警舰发出求救信号,并向海警舰靠拢,海警舰立即沿正西方向对货轮实施救援,此时距货轮200海里,并测得海盗船位于海警舰北偏西60°方向的C处.
(1)求海盗船所在C处距货轮航线AB的距离.
(2)若货轮以45海里/时的速度在A处沿正东方向海警舰靠拢,海盗以50海里/时的速度由C处沿正南方向对货轮进行拦截,问海警舰的速度应为多少时才能抢在海盗之前去救货轮?(结果保留根号)
相关知识点
推荐套卷
 =0有实根的概率.(用列表法或画树形图法解,A代表数字1)
=0有实根的概率.(用列表法或画树形图法解,A代表数字1)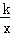 (k≠0)的图象过等边三角形AOB的顶点A,已知点B(﹣2,0)
(k≠0)的图象过等边三角形AOB的顶点A,已知点B(﹣2,0)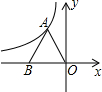
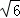 x+3=0;
x+3=0;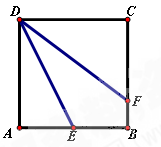
 粤公网安备 44130202000953号
粤公网安备 44130202000953号