如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB= ,AD=1.
,AD=1.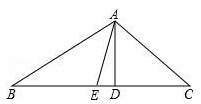
(1)求BC的长;
(2)求tan∠DAE的值.
如图,在正方形 中,点 在对角线 上(不与点 , 重合), 于点 , 于点 ,连接 .
(1)写出线段 , , 长度之间的数量关系,并说明理由;
(2)若正方形 的边长为1, ,求线段 的长.

如图, 已知四边形 是菱形, 于点 , 于点 .
(1) 求证: ;
(2) 若 , ,求 的值 .

如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120m.试求大楼AB的高度(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,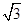 ≈1.73)
≈1.73)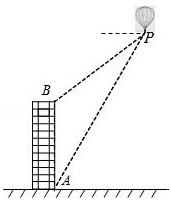
如图,某中学操场边有一旗杆A,小明在操场的C处放风筝,风筝飞在图中的D处,在CA的延长线上离小明30米远的E处的小刚发现自己的位置与风筝D和旗杆的顶端B在同一条直线上,小刚在E处测得旗杆顶点B的仰角为 ,且tan
,且tan =
= ,小明在C处测得旗杆顶点B的仰角为45°.
,小明在C处测得旗杆顶点B的仰角为45°.
(1)求旗杆的高度.
(2)此时,在C处背向旗杆,测得风筝D的仰角(即∠DCF)为48°,求风筝D离地面的距离.(结果精确到0.1米,其中sin48°≈0.74, cos48°≈0.67,tan48°≈1.11)
如图所示,在平面直角坐标系 中,等腰 的边 与反比例函数 的图象相交于点 ,其中 ,点 在 轴的正半轴上,点 的坐标为 ,过点 作 轴于点 .
(1)已知一次函数的图象过点 , ,求该一次函数的表达式;
(2)若点 是线段 上的一点,满足 ,过点 作 轴于点 ,连结 ,记 的面积为 ,设 ,
①用 表示 (不需要写出 的取值范围);
②当 取最小值时,求 的值.

如图,AB是⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.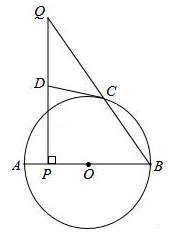
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由;
(2)若cosB= ,AP=1,求QC的长.
,AP=1,求QC的长.
如图, 是 的直径, 切 于点 ,连接 ,作 交 于点 , 的延长线与 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 的半径为1, ,求 的长.

如图,一艘货轮在A处发现其北偏东45°方向有一海盗船,立即向位于正东方向B处的海警舰发出求救信号,并向海警舰靠拢,海警舰立即沿正西方向对货轮实施救援,此时距货轮200海里,并测得海盗船位于海警舰北偏西60°方向的C处.
(1)求海盗船所在C处距货轮航线AB的距离.
(2)若货轮以45海里/时的速度在A处沿正东方向海警舰靠拢,海盗以50海里/时的速度由C处沿正南方向对货轮进行拦截,问海警舰的速度应为多少时才能抢在海盗之前去救货轮?(结果保留根号)
如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的高度.她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1∶1的斜坡步行15分钟到达C处,此时,测得点A的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出娱乐场地所在山坡AE的高度AB.(精确到0.1米,参考数据: ≈1.41).
≈1.41).
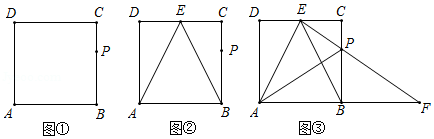
如图,在矩形 中, , , 是 边上的一点,且 .
(1)用尺规在图①中作出 边上的中点 ,连接 、 (保留作图痕迹,不写作法);
(2)如图②,在(1)的条件下,判断 是否平分 ,并说明理由;
(3)如图③,在(2)的条件下,连接 并延长交 的延长线于点 ,连接 ,不添加辅助线, 能否由都经过 点的两次变换与 组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求sinB的值.
,求sinB的值.
如图,晚上小明站在路灯P的底下观察自己的影子时发现,当他站在F点的位置时,在地面上的影子为BF,小明向前走2米到D点时,在地面上的影子为AD,若AB=4米,∠PBF=60°,∠PAB=30°,通过计算,求出小明的身高.(结果保留根号).