初中数学解直角三角形解答题

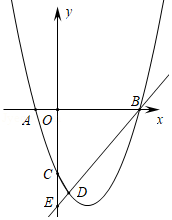
如图，抛物线与轴交于，，，两点，与轴交于点，且．

（1）求抛物线的解析式；

（2）若，，，是抛物线上的两点，当，时，均有，求的取值范围；

（3）抛物线上一点，直线与轴交于点，动点在线段上，当时，求点的坐标．

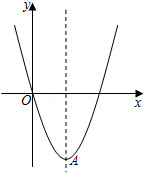
如图①，抛物线与轴交于点，与轴交于点，，将直线绕点逆时针旋转，所得直线与轴交于点．

（1）求直线的函数解析式；

（2）如图②，若点是直线上方抛物线上的一个动点

①当点到直线的距离最大时，求点的坐标和最大距离；

②当点到直线的距离为时，求的值．

如图1，抛物线经过点、两点，是其顶点，将抛物线绕点旋转，得到新的抛物线．

（1）求抛物线的函数解析式及顶点的坐标；

（2）如图2，直线经过点，是抛物线上的一点，设点的横坐标为，连接并延长，交抛物线于点，交直线于点，若，求的值；

（3）如图3，在（2）的条件下，连接、，在直线下方的抛物线上是否存在点，使得？若存在，求出点的横坐标；若不存在，请说明理由．

如图，在平面直角坐标系中，抛物线经过原点，顶点为．

（1）求抛物线的函数解析式；

（2）设点为抛物线的对称轴上的一点，点在该抛物线上，当四边

形为菱形时，求出点的坐标；

（3）在（2）的条件下，抛物线在第一象限的图象上是否存在一点，使得点到直线的距离与其到轴的距离相等？若存在，求出直线的函数解析式；若不存在，请说明理由．

如图一，在射线的一侧以为一条边作矩形，，，点是线段上一动点（不与点重合），连结，过点作的垂线交射线于点，连接．

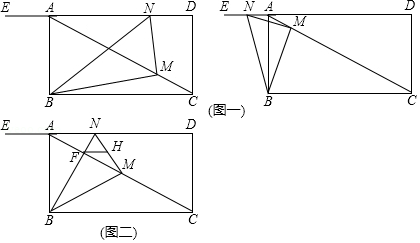
（1）求的大小；

（2）问题探究：动点在运动的过程中，

①是否能使为等腰三角形，如果能，求出线段的长度；如果不能，请说明理由．

②的大小是否改变？若不改变，请求出的大小；若改变，请说明理由．

（3）问题解决：

如图二，当动点运动到的中点时，与的交点为，的中点为，求线段的长度．

已知抛物线与轴分别交于，两点，与轴交于点．

（1）求抛物线的表达式及顶点的坐标；

（2）点是线段上一个动点．

①如图1，设，当为何值时，？

②如图2，以，，为顶点的三角形是否与相似？若相似，求出点的坐标；若不相似，请说明理由．

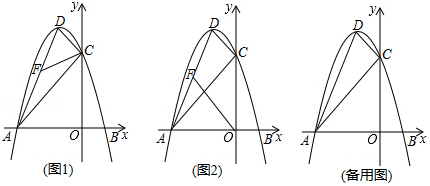
如图1，抛物线与抛物线相交轴于点，抛物线与轴交于、两点（点在点的右侧），直线交轴负半轴于点，交轴于点，且．

（1）求抛物线的解析式与的值；

（2）抛物线的对称轴交轴于点，连接，在轴上方的对称轴上找一点，使以点，，为顶点的三角形与相似，求出的长；

（3）如图2，过抛物线上的动点作轴于点，交直线于点，若点是点关于直线的对称点，是否存在点（不与点重合），使点落在轴上？若存在，请直接写出点的横坐标，若不存在，请说明理由．

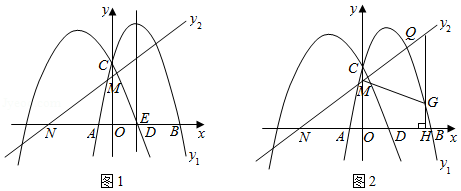
如图，建筑物AB后有一座假山，其坡度为i=1：，山坡上E点处有一凉亭，测得假山坡脚C与建筑物水平距离BC=25米，与凉亭距离CE=20米，某人从建筑物顶端测得E点的俯角为45°，求建筑物AB的高．（注：坡度i是指坡面的铅直高度与水平宽度的比）

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle \mathit{BAC}=90°$， $\mathit{AB}=\mathit{AC}$，点 $D$是 $\mathit{BC}$边上一动点，连接 $\mathit{AD}$，把 $\mathit{AD}$绕点 $A$逆时针旋转 $90°$，得到 $\mathit{AE}$，连接 $\mathit{CE}$， $\mathit{DE}$．点 $F$是 $\mathit{DE}$的中点，连接 $\mathit{CF}$．

（1）求证： $\mathit{CF}=\frac{\sqrt{2}}{2}\mathit{AD}$；

（2）如图2所示，在点 $D$运动的过程中，当 $\mathit{BD}=2\mathit{CD}$时，分别延长 $\mathit{CF}$， $\mathit{BA}$，相交于点 $G$，猜想 $\mathit{AG}$与 $\mathit{BC}$存在的数量关系，并证明你猜想的结论；

（3）在点 $D$运动的过程中，在线段 $\mathit{AD}$上存在一点 $P$，使 $\mathit{PA}+\mathit{PB}+\mathit{PC}$的值最小．当 $\mathit{PA}+\mathit{PB}+\mathit{PC}$的值取得最小值时， $\mathit{AP}$的长为 $m$，请直接用含 $m$的式子表示 $\mathit{CE}$的长．

如图，矩形 $\mathit{ABCD}$ 中，点 $P$ 为对角线 $\mathit{AC}$ 所在直线上的一个动点，连接 $\mathit{PD}$ ，过点 $P$ 作 $\mathit{PE}\perp \mathit{PD}$ ，交直线 $\mathit{AB}$ 于点 $E$ ，过点 $P$ 作 $\mathit{MN}\perp \mathit{AB}$ ，交直线 $\mathit{CD}$ 于点 $M$ ，交直线 $\mathit{AB}$ 于点 $N$ ． $\mathit{AB}=4\sqrt{3}$ ， $\mathit{AD}=4$ ．

（1）如图1，①当点 $P$ 在线段 $\mathit{AC}$ 上时， $\angle \mathit{PDM}$ 和 $\angle \mathit{EPN}$ 的数量关系为： $\angle \mathit{PDM}$    $\angle \mathit{EPN}$ ；

② $\frac{\mathit{DP}}{\mathit{PE}}$ 的值是 　　；

（2）如图2，当点 $P$ 在 $\mathit{CA}$ 延长线上时，（1）中的结论②是否成立？若成立，请证明；若不成立，说明理由；

（3）如图3，以线段 $\mathit{PD}$ ， $\mathit{PE}$ 为邻边作矩形 $\mathit{PEFD}$ ．设 $\mathit{PM}$ 的长为 $x$ ，矩形 $\mathit{PEFD}$ 的面积为 $y$ ．请直接写出 $y$ 与 $x$ 之间的函数关系式及 $y$ 的最小值．

在平面直角坐标系中，抛物线 $y=a{x}^2+\mathit{bx}+3$与 $x$轴交于点 $A(-3,0)$、 $B(1,0)$，交 $y$轴于点 $N$，点 $M$为抛物线的顶点，对称轴与 $x$轴交于点 $C$．

（1）求抛物线的解析式；

（2）如图1，连接 $\mathit{AM}$，点 $E$是线段 $\mathit{AM}$上方抛物线上一动点， $\mathit{EF}\perp \mathit{AM}$于点 $F$，过点 $E$作 $\mathit{EH}\perp x$轴于点 $H$，交 $\mathit{AM}$于点 $D$．点 $P$是 $y$轴上一动点，当 $\mathit{EF}$取最大值时：

①求 $\mathit{PD}+\mathit{PC}$的最小值；

②如图2， $Q$点为 $y$轴上一动点，请直接写出 $\mathit{DQ}+\frac{1}{4}\mathit{OQ}$的最小值．

如图， $\mathit{AC}$ 是 $\odot O$ 的直径， $\mathit{BC}$ ， $\mathit{BD}$ 是 $\odot O$ 的弦， $M$ 为 $\mathit{BC}$ 的中点， $\mathit{OM}$ 与 $\mathit{BD}$ 交于点 $F$ ，过点 $D$ 作 $\mathit{DE}\perp \mathit{BC}$ ，交 $\mathit{BC}$ 的延长线于点 $E$ ，且 $\mathit{CD}$ 平分 $\angle \mathit{ACE}$ ．

（1）求证： $\mathit{DE}$ 是 $\odot O$ 的切线；

（2）求证： $\angle \mathit{CDE}=\angle \mathit{DBE}$ ；

（3）若 $\mathit{DE}=6$ ， $\tan \angle \mathit{CDE}=\frac{2}{3}$ ，求 $\mathit{BF}$ 的长．

问题背景: 如图（a），点A、B在直线l的同侧，要在直线l上找一点C，使AC与BC的距离之和最小，我们可以作出点B关于l的对称点B′，连接AB′与直线l交于点C，则点C即为所求．

实践运用： 如图(b)，已知，⊙O的直径CD为4，点A 在⊙O 上，∠ACD = 30°，B 为弧AD 的中点，P为直径CD上一动点，求：PA+ PB的最小值，并写出解答过程．

知识拓展：如图(c)，在菱形ABCD中，AB = 10，∠DAB= 60°，P是对角线AC上一动点，E、F分别是线段AB和BC上的动点，则PE +PF的最小值是     ．（直接写出答案）

点P在图形M上, 点Q在图形N上,记为线段PQ长度的最大值，为线段PQ长度的最小值，图形M，N的平均距离．
（1）在平面直角坐标系中，⊙O是以O为圆心，2的半径的圆，且A，B，求及；(直接写出答案即可)
（2）半径为1的⊙C的圆心C与坐标原点O重合，直线与轴交于点D，与轴交于点F，记线段DF为图形G，求；
（3）在（2）的条件下，如果⊙C的圆心C从原点沿轴向右移动，⊙C的半径不变，且，求圆心C的横坐标．

（本题12分）如图，过点A（0，3）的直线l₁与x轴交于点B，tan∠ABO=．过点A的另一直线l₂：y＝－x＋b (t＞0)与x轴交于点Q，点P是射线AB上的一个动点，过P作PH⊥x轴于点H，设PB＝5t．

（1）求直线l₁ 的函数解析式；
（2）当点P在线段AB上运动时，设△PHQ的面积为S（S≠0），求S与t之间的函数关系式（要求写出自变量t的取值范围）；
（3）当点P 在射线AB上运动时，是否存在这样的t值，使以P，H，Q为顶点的三角形与△AOQ相似？若存在，直接写出所有满足条件的t值所对应的P点坐标；若不存在，请说明理由．