初中数学解直角三角形解答题

如图，在△ABC中，AB=AC，∠B=30°，BC=8，D在边BC上，E在线段DC上，DE=4，△DEF是等边三角形，边DF交边AB于点M，边EF交边AC于点N．

（1）求证：△BMD∽△CNE；
（2）当BD为何值时，以M为圆心，以MF为半径的圆与BC相切？
（3）设BD=x，五边形ANEDM的面积为y，求y与x之间的函数解析式及自变量x的取值范围；当x为何值时，y有最大值？并求出y的最大值．

（本题满分14分 第（1）小题4分，第（2）小题4分，第（3）小题6分）
已知：如图，在△ABC中，AB＝AC＝15， cos∠A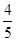＝．点M在AB边上，AM＝2MB，点P是边AC上的一个动点，设PA＝x．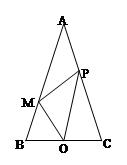

（1）求底边BC的长；
（2）若点O是BC的中点，联接MP、MO、OP，设四边形AMOP的面积是y，求y关于x的函数关系式，并出写出x的取值范围；
（3）把△MPA沿着直线MP翻折后得到△MPN，是否可能使△MPN的一条边（折痕边PM除外）与AC垂直？若存在，请求出x的值；若不存在，请说明理由．

如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，∠CBA=32°，求∠EFD的度数。    

已知，如图①，∠MON=60°，点A、B为射线OM、ON上的动点（点A、B不与点O重合），且AB=，在∠MON的内部、△AOB的外部有一点P，且AP=BP，∠APB=120°.
 
（1）求AP的长；
（2）求证：点P在∠MON的平分线上；
（3）如图②，点C，D，E，F分别是四边形AOBP的边AO，OB，BP，PA的中点，连接CD，DE，EF，FC，OP.
①当AB⊥OP时，请直接写出四边形CDEF的周长；
②若四边形CDEF的周长用t表示，请直接写出t的取值范围．

如图，二次函数 $y_1=a{(x-m)}^2+n$ ， $y_2=6a{x}^2+n(a<0$ ， $m>0$ ， $n>0)$ 的图象分别为 $C_1$ 、 $C_2$ ， $C_1$ 交 $y$ 轴于点 $P$ ，点 $A$ 在 $C_1$ 上，且位于 $y$ 轴右侧，直线 $\mathit{PA}$ 与 $C_2$ 在 $y$ 轴左侧的交点为 $B$ ．

（1）若 $P$ 点的坐标为 $(0,2)$ ， $C_1$ 的顶点坐标为 $(2,4)$ ，求 $a$ 的值；

（2）设直线 $\mathit{PA}$ 与 $y$ 轴所夹的角为 $\alpha$ ．

①当 $\alpha =45°$ ，且 $A$ 为 $C_1$ 的顶点时，求 $\mathit{am}$ 的值；

②若 $\alpha =90°$ ，试说明：当 $a$ 、 $m$ 、 $n$ 各自取不同的值时， $\frac{\mathit{PA}}{\mathit{PB}}$ 的值不变；

（3）若 $\mathit{PA}=2\mathit{PB}$ ，试判断点 $A$ 是否为 $C_1$ 的顶点？请说明理由．

如图，防洪大堤的横断面是梯形ABCD，其中AD∥BC，坡角α=60⁰，汛期来临前对其进行了加固，改造后的背水面坡角β=45⁰，若原坡长AB=20m，求改造后的坡长AE（结果保留根号）

在平面直角坐标系中，抛物线 $y=-x^2+\mathit{kx}-2k$ 的顶点为 $N$ ．

（1）若此抛物线过点 $A(-3,1)$ ，求抛物线的解析式；

（2）在（1）的条件下，若抛物线与 $y$ 轴交于点 $B$ ，连接 $\mathit{AB}$ ， $C$ 为抛物线上一点，且位于线段 $\mathit{AB}$ 的上方，过 $C$ 作 $\mathit{CD}$ 垂直 $x$ 轴于点 $D$ ， $\mathit{CD}$ 交 $\mathit{AB}$ 于点 $E$ ，若 $\mathit{CE}=\mathit{ED}$ ，求点 $C$ 坐标；

（3）已知点 $M(2-\frac{4\sqrt{3}}{3}$ ， $0)$ ，且无论 $k$ 取何值，抛物线都经过定点 $H$ ，当 $\angle \mathit{MHN}=60°$ 时，求抛物线的解析式．

如图，在平面直角坐标系中，直线 $y=-\frac{1}{2}x+2$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，抛物线 $y=-\frac{2}{3}{x}^2+\mathit{bx}+c$ 过点 $B$ 且与直线相交于另一点 $C(\frac{5}{2}$ ， $\frac{3}{4})$ ．

（1）求抛物线的解析式；

（2）点 $P$ 是抛物线上的一动点，当 $\angle \mathit{PAO}=\angle \mathit{BAO}$ 时，求点 $P$ 的坐标；

（3）点 $N(n$ ， $0\left)\right(0<n<\frac{5}{2})$ 在 $x$ 轴的正半轴上，点 $M(0,m)$ 是 $y$ 轴正半轴上的一动点，且满足 $\angle \mathit{MNC}=90°$ ．

①求 $m$ 与 $n$ 之间的函数关系式；

②当 $m$ 在什么范围时，符合条件的 $N$ 点的个数有2个？

如图1，在平面直角坐标系中， $O$ 是坐标原点，抛物线 $y=\frac{1}{2}{x}^2+\mathit{bx}+c$ 经过点 $B(6,0)$ 和点 $C(0,-3)$ ．

（1）求抛物线的表达式；

（2）如图2，线段 $\mathit{OC}$ 绕原点 $O$ 逆时针旋转 $30°$ 得到线段 $\mathit{OD}$ ．过点 $B$ 作射线 $\mathit{BD}$ ，点 $M$ 是射线 $\mathit{BD}$ 上一点（不与点 $B$ 重合），点 $M$ 关于 $x$ 轴的对称点为点 $N$ ，连接 $\mathit{NM}$ ， $\mathit{NB}$ ．

①直接写出 $\mathit{\Delta MBN}$ 的形状为 　 　；

②设 $\mathit{\Delta MBN}$ 的面积为 $S_1$ ， $\mathit{\Delta ODB}$ 的面积为是 $S_2$ ．当 $S_1=\frac{2}{3}{S}_2$ 时，求点 $M$ 的坐标；

（3）如图3，在（2）的结论下，过点 $B$ 作 $\mathit{BE}\perp \mathit{BN}$ ，交 $\mathit{NM}$ 的延长线于点 $E$ ，线段 $\mathit{BE}$ 绕点 $B$ 逆时针旋转，旋转角为 $\alpha (0°<\alpha <120°)$ 得到线段 $\mathit{BF}$ ，过点 $F$ 作 $\mathit{FK}//x$ 轴，交射线 $\mathit{BE}$ 于点 $K$ ， $\angle \mathit{KBF}$ 的角平分线和 $\angle \mathit{KFB}$ 的角平分线相交于点 $G$ ，当 $\mathit{BG}=2\sqrt{3}$ 时，请直接写出点 $G$ 的坐标为 　　．

如图，我边防哨所A测得一走私船在A的西北方向B处由南向北正以每小时10海里的速度逃
跑，我缉私艇迅速朝A的西偏北60⁰的方向出水拦截，2小时后终于在B地正北方向M处拦截住，试求缉私
船的速度．（参考数据：）

丽水市在规划新城期间，欲拆除瓯江岸边的一根电线杆AB(如图)，已知距电线杆AB水平距离14米处是河岸，即BD＝14米，该河岸的坡面CD的坡角∠CDF的正切值为2（即tan∠CDF=2），岸高CF为2米，在坡顶C处测得杆顶A的仰角为30°，D、E之间是宽2米的人行道，请你通过计算说明在拆除电线杆AB时，为确保安全，是否将此人行道封上？(在地面上以点B为圆心，以AB长为半径的圆形区域为危险区域)

在矩形ABCD中，，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．
（1）如图1，当DH=DA时，
①填空：∠HGA=       度；
②若EF∥HG，求∠AHE的度数，并求此时a的最小值；
（2）如图3，∠AEH=60°，EG=2BG，连接FG，交边FG，交边DC于点P，且FG⊥AB，G为垂足，求a的值．

已知Rt△ABC中，AB是⊙O的弦，斜边AC交⊙O于点D，且AD=DC，延长CB交⊙O于点E．

（1）图1的A、B、C、D、E五个点中，是否存在某两点间的距离等于线段CE的长？请说明理由；
（2）如图2，过点E作⊙O的切线，交AC的延长线于点F．
①若CF=CD时，求sin∠CAB的值；
②若CF=aCD（a＞0）时，试猜想sin∠CAB的值．（用含a的代数式表示，直接写出结果）

如图，是的直径，、两点在的延长线上，是上的点，且，延长至，使得，设，．

（1）求证：；

（2）求，的长；

（3）若点在、、三点确定的圆上，求的长．

如图一，在射线的一侧以为一条边作矩形，，，点是线段上一动点（不与点重合），连结，过点作的垂线交射线于点，连接．

（1）求的大小；

（2）问题探究：动点在运动的过程中，

①是否能使为等腰三角形，如果能，求出线段的长度；如果不能，请说明理由．

②的大小是否改变？若不改变，请求出的大小；若改变，请说明理由．

（3）问题解决：

如图二，当动点运动到的中点时，与的交点为，的中点为，求线段的长度．