[上海]2013届上海市闸北区中考一模数学试卷
抛物线y=-x2向左平移2个单位后所得的抛物线解析式是( )
| A.y=-x2-2; | B.y=-(x-2)2; |
| C.y=-(x+2)2; | D.y=-x2+2. |
已知D、E分别在△ABC的BA、CA的延长线上,下列给出的条件中能判定ED∥BC的是( )
(A)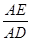 =
=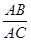 ; (B)
; (B)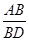 =
=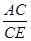 ;
;
(C)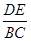 =
=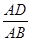 ; (D)
; (D)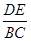 =
= .
.
在△ABC中,中线AD、BE相交于点O,且S△BOD=5,则△ABC的面积是( )
(A)30; (B)20; (C)15; (D)5.
根据二次函数y=-x2+2x+3的图像,判断下列说法中,错误的是( )
| A.二次函数图像的对称轴是直线x=1; |
| B.当x>0时,y<4; |
| C.当x≤1时,函数值y是随着x的增大而增大; |
| D.当y≥0时,x的取值范围是-1≤x≤3时. |
钓鱼岛列岛是我国最早发现、命名,并行使主权的.在一幅比例尺是1︰100000的地图上,测得钓鱼岛的东西走向长为3.5厘米,那么它的东西走向实际长大约为 米.
某印刷厂一月份印书50万册,如果从二月份起,每月印书量的增长率都为x,那么三月份的印书量y(万册)与x的函数解析式是 .
如图,已知点D、E分别在△ABC的边AB和AC上,且DE∥BC,S△AED︰S梯形EDBC=1︰2,则AE︰AC的比值是 .
如图,在Rt△ABC中,∠C=90°,点D在边BC上,且∠ADC+∠B=90°,DC=3,BD=6,则cosB= .
如图,在△ABC中,AB=AC,∠A=36°, BD平分∠ABC交AC于点D,DE平分∠BDC交BC于点E,则 = .
= .
如图,在Rt△ABC中,AB=6cm,BC=4cm,点D是斜边AB上的中点,把△ADC沿着AB方向平移1cm得△EFP,EP与FP分别交边BC于点H和点G,则GH= .
(本题满分10分 第(1)小题4分,第(2)小题6分)
已知:二次函数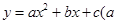 ≠0的图像经过点(3,5)、(2,8)、(0,8).
≠0的图像经过点(3,5)、(2,8)、(0,8).
(1)求这个二次函数的解析式;
(2)已知抛物线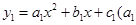 ≠0,
≠0,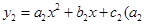 ≠0,且满足
≠0,且满足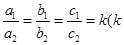 ≠0,1,则我们称抛物线
≠0,1,则我们称抛物线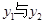 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当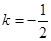 时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
已知:如图六,九年级某班同学要测量校园内旗杆CH的高度,在地面的点E处用测角器测得旗杆顶点C的仰角∠CAD=45°,再沿直线EF向着旗杆方向行走10米到点F处,在点F又用测角器测得旗杆顶点C的仰角∠CBA=60°;已知测角器的高度为1.6米,求旗杆CH的高度(结果保留根号).
已知:如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点M、N分别在边AO和边OD上,且AM=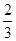 AO,ON=
AO,ON=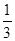 OD,设
OD,设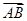 =
=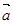 ,
,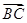 =
=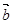 ,试用
,试用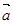 、
、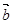 的线性组合表示向量
的线性组合表示向量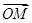 和向量
和向量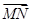 .
.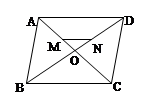
(本题满分12分 第(1)小题6分,第(2)小题6分)
已知:如图,在△ABC中,BD⊥AC于点D, CE⊥AB于点E,EC和BD相交于点O,联接DE. 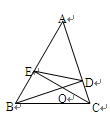
(1)求证:△EOD∽△BOC;
(2)若S△EOD=16,S△BOC=36,求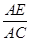 的值.
的值.
(本题满分12分 第(1)小题6分,第(2)小题6分)
已知:如图,二次函数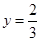 x2
x2 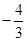 x
x 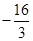 的图像与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为Q,直线QB与y轴交于点E.
的图像与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为Q,直线QB与y轴交于点E.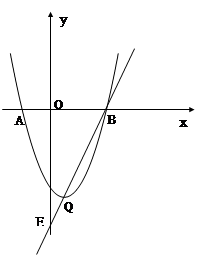
(1)求点E的坐标;
(2)在x轴上方找一点C,使以点C、O、B为顶点的三角形与△BOE相似,请直接写出点C的坐标.
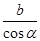 ;
;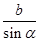 ;
;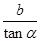 ;
;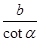 .
.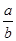 =
=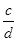 ,m>0,则下列式子中,成立的是( )
,m>0,则下列式子中,成立的是( )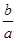 =
=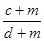 ;
;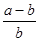 =
=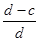 ;
;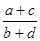 =
= +
+ =2(
=2(
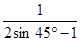 -2
-2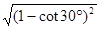 +sin260°+cos260°.
+sin260°+cos260°.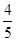 .点M在AB边上,AM=2MB,点P是边AC上的一个动点,设PA=x.
.点M在AB边上,AM=2MB,点P是边AC上的一个动点,设PA=x.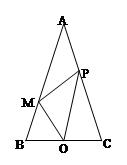
 粤公网安备 44130202000953号
粤公网安备 44130202000953号