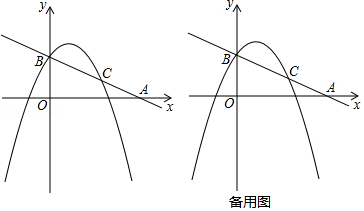
如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,抛物线 过点 且与直线相交于另一点 , .
(1)求抛物线的解析式;
(2)点 是抛物线上的一动点,当 时,求点 的坐标;
(3)点 , 在 轴的正半轴上,点 是 轴正半轴上的一动点,且满足 .
①求 与 之间的函数关系式;
②当 在什么范围时,符合条件的 点的个数有2个?
相关知识点
推荐套卷
如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,抛物线 过点 且与直线相交于另一点 , .
(1)求抛物线的解析式;
(2)点 是抛物线上的一动点,当 时,求点 的坐标;
(3)点 , 在 轴的正半轴上,点 是 轴正半轴上的一动点,且满足 .
①求 与 之间的函数关系式;
②当 在什么范围时,符合条件的 点的个数有2个?
