[江苏]2014届江苏省无锡市滨湖区九年级上学期期中考试数学试卷
要使二次根式 有意义,字母x必须满足的条件是( )
有意义,字母x必须满足的条件是( )
| A.x≥1 | B.x -1 -1 |
C.x≥-1 | D.x 1 1 |
若一元二次方程x2+x-2=0的解为x1、x2,则x1•x2的值是( )
| A.1 | B.—1 | C.2 | D.—2 |
目前我国建立了比较完善的经济困难学生资助体系.某校去年上半年发放给每个经济困难学生389元,今年上半年发放了438元,设每半年发放的资助金额的平均增长率为 ,则下面列出的方程中正确的是( )
,则下面列出的方程中正确的是( )
A. |
B.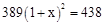 |
C. |
D. |
顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( )
| A.菱形 | B.矩形 |
| C.对角线互相垂直的四边形 | D.对角线相等的四边形 |
有下列说法:①弦是直径 ②半圆是弧 ③圆中最长的弦是直径 ④半圆是圆中最长的弧 ⑤平分弦的直径垂直于弦,其中正确的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC,则下列结论不一定成立的是( )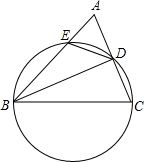
A.BD⊥AC B.AC2=2AB·AE
C.BC=2AD D.△ADE是等腰三角形
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=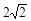 ,那么AC的长等于( )
,那么AC的长等于( )
| A.12 | B.7 | C. |
D. |
如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是1和3,则正方形的边长是 .
如图,数轴上半径为1的⊙O从原点O开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P以每秒2个单位的速度向左运动,经过 秒后,点P在⊙O上.
已知关于x的方程 .
.
(1)求证:无论k取什么实数值,这个方程总有实数根;
(2)当 =3时,△ABC的每条边长恰好都是方程
=3时,△ABC的每条边长恰好都是方程 的根,求△ABC的周长.
的根,求△ABC的周长.
某中学开展“中国梦、我的梦”演讲比赛,甲、乙两班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
(1)根据下图,分别求出两班复赛的平均成绩和方差;
(2)根据(1)的计算结果,分析哪个班级的复赛成绩较好?
如图,点E、F分别是 ABCD的边BC、AD上的点,且BE=DF.
ABCD的边BC、AD上的点,且BE=DF.

(1)求证:四边形AECF是平行四边形;
(2)若AE=BE,∠BAC=90°,试判断四边形AECF的形状,并说明理由.
“惠民”经销店为某工厂代销一种工业原料(代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨;该经销店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨工业原料共需支付厂家及其它费用100元.
(1)当每吨售价是240元时,计算此时的月销售量;
(2)若在“薄利多销、让利于民”的原则下,当每吨原料售价为多少时,该店的月利润为9000元;
(3)每吨原料售价为多少时,该店的月利润最大,求出最大利润.
如图,⊙O的弦AB=8,直径CD⊥AB于M,OM :MD ="3" :2, E是劣弧CB上一点,连结CE并延长交CE的延长线于点F.

求:(1)⊙O的半径;
(2)求CE·CF的值.
问题背景: 如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接AB′与直线l交于点C,则点C即为所求.
实践运用: 如图(b),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD = 30°,B 为弧AD 的中点,P为直径CD上一动点,求:PA+ PB的最小值,并写出解答过程.
知识拓展:如图(c),在菱形ABCD中,AB = 10,∠DAB= 60°,P是对角线AC上一动点,E、F分别是线段AB和BC上的动点,则PE +PF的最小值是 .(直接写出答案)




 时,原方程应变形为( )
时,原方程应变形为( )



 化成一般形式为 .
化成一般形式为 . 与
与 是同类二次根式,则
是同类二次根式,则 = .
= . 有一个解是0,则m= .
有一个解是0,则m= .
 (2)
(2) (3)
(3)
 时,求
时,求 的值.
的值.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号