如图,点E、F分别是 ABCD的边BC、AD上的点,且BE=DF.
ABCD的边BC、AD上的点,且BE=DF.
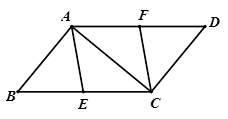
(1)求证:四边形AECF是平行四边形;
(2)若AE=BE,∠BAC=90°,试判断四边形AECF的形状,并说明理由.
相关知识点
推荐套卷
如图,点E、F分别是 ABCD的边BC、AD上的点,且BE=DF.
ABCD的边BC、AD上的点,且BE=DF.

(1)求证:四边形AECF是平行四边形;
(2)若AE=BE,∠BAC=90°,试判断四边形AECF的形状,并说明理由.