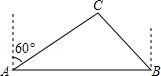
如图,随着我市铁路建设进程的加快,现规划从 地到 地有一条笔直的铁路通过,但在附近的 处有一大型油库,现测得油库 在 地的北偏东 方向上,在 地的西北方向上, 的距离为 米.已知在以油库 为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库 是否会受到影响?请说明理由.
相关知识点
推荐套卷
如图,随着我市铁路建设进程的加快,现规划从 地到 地有一条笔直的铁路通过,但在附近的 处有一大型油库,现测得油库 在 地的北偏东 方向上,在 地的西北方向上, 的距离为 米.已知在以油库 为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库 是否会受到影响?请说明理由.
