初中数学解直角三角形解答题

如图，在Rt△ABC中，∠C=90°，AB的垂直平分线与AC，AB的交点分别为D，E．

（1）若AD=15，，求AC的长和的值；
（2）若，求的值．（结果保留根号）

如图，晚上小明站在路灯P的底下观察自己的影子时发现，当他站在F点的位置时，在地面上的影子为BF，小明向前走2米到D点时，在地面上的影子为AD，若AB=4米，∠PBF=60°，∠PAB=30°，通过计算，求出小明的身高．（结果保留根号）．

图①、②分别是某种型号跑步机的实物图与示意图，已知踏板CD长为1．6m，CD与地面DE的夹角∠CDE为12°，支架AC长为0．8m，∠ACD为80°，求跑步机手柄的一端A的高度h（精确到0．1m）．
（参考数据：sin12°=cos78°≈0．21，sin68°=cos22°≈0．93，tan68°≈2．48）

如图， $\odot O$的半径为 $R$，其内接锐角三角形 $\mathit{ABC}$中， $\angle A$、 $\angle B$、 $\angle C$所对的边分别是 $a$、 $b$、 $c$．

（1）求证： $\frac{a}{\sin \angle A}=\frac{b}{\sin \angle B}=\frac{c}{\sin \angle C}=2R$；

（2）若 $\angle A=60°$， $\angle C=45°$， $\mathit{BC}=4\sqrt{3}$，利用（1）的结论求 $\mathit{AB}$的长和 $\sin \angle B$的值．

如图，某校一大楼的高为米，不远处有一水塔．某同学在楼底处测得塔顶处的仰角为，在楼顶点测得塔顶处的仰角为．求的高度(结果精确到米) ．（参考数据：，，，，，）

小华同学学习了第二十五章《锐角三角比》后，对求三角形的面积方法进行了研究，得到了新的结论：如图，已知锐角△ABC，则

（1）试证明上述结论；
（2）运用这个新的结论，请完成下题：如图，在等腰△ABC中，AB=AC=12厘米，点P从A点出发，沿着边AB移动，点Q从C点出发沿着边CA移动，点Q的速度是1厘米/秒，点P的速度是点Q速度的2倍，若它们同时出发，设移动时间为t秒，问：当t为何值时，?

如图，在 $▱\mathit{ABCD}$ 中， $E$ ， $F$ 是对角线 $\mathit{BD}$ 上的两点（点 $E$ 在点 $F$ 左侧），且 $\angle \mathit{AEB}=\angle \mathit{CFD}=90°$ ．

（1）求证：四边形 $\mathit{AECF}$ 是平行四边形；

（2）当 $\mathit{AB}=5$ ， $\tan \angle \mathit{ABE}=\frac{3}{4}$ ， $\angle \mathit{CBE}=\angle \mathit{EAF}$ 时，求 $\mathit{BD}$ 的长．

如图，已知 $\mathit{AB}$ 是 $\odot O$ 的直径， $\angle \mathit{ACD}$ 是 $\widehat{\mathit{AD}}$ 所对的圆周角， $\angle \mathit{ACD}=30°$ ．

（1）求 $\angle \mathit{DAB}$ 的度数；

（2）过点 $D$ 作 $\mathit{DE}\perp \mathit{AB}$ ，垂足为 $E$ ， $\mathit{DE}$ 的延长线交 $\odot O$ 于点 $F$ ．若 $\mathit{AB}=4$ ，求 $\mathit{DF}$ 的长．

如图，已知点 $C$ 是以 $\mathit{AB}$ 为直径的半圆上一点， $D$ 是 $\mathit{AB}$ 延长线上一点，过点 $D$ 作 $\mathit{BD}$ 的垂线交 $\mathit{AC}$ 的延长线于点 $E$ ，连结 $\mathit{CD}$ ，且 $\mathit{CD}=\mathit{ED}$ ．

（1）求证： $\mathit{CD}$ 是 $\odot O$ 的切线；

（2）若 $\tan \angle \mathit{DCE}=2$ ， $\mathit{BD}=1$ ，求 $\odot O$ 的半径．

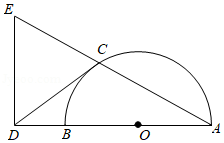
数学小组研究如下问题：长春市的纬度约为北纬 $44°$ ，求北纬 $44°$ 纬线的长度，小组成员查阅了相关资料，得到三条信息：

（1）在地球仪上，与南，北极距离相等的大圆圈，叫赤道，所有与赤道平行的圆圈叫纬线；

（2）如图， $\odot O$ 是经过南、北极的圆，地球半径 $\mathit{OA}$ 约为 $6400\mathit{km}$ ．弦 $\mathit{BC}//\mathit{OA}$ ，过点 $O$ 作 $\mathit{OK}\perp \mathit{BC}$ 于点 $K$ ，连接 $\mathit{OB}$ ．若 $\angle \mathit{AOB}=44°$ ，则以 $\mathit{BK}$ 为半径的圆的周长是北纬 $44°$ 纬线的长度；

（3）参考数据： $\pi$ 取3， $\sin 44°=0.69$ ， $\cos 44°=0.72$ ．

小组成员给出了如下解答，请你补充完整：

解：因为 $\mathit{BC}//\mathit{OA}$ ， $\angle \mathit{AOB}=44°$ ，

所以 $\angle B=\angle \mathit{AOB}=44°($ 　　 $)$ （填推理依据），

因为 $\mathit{OK}\perp \mathit{BC}$ ，所以 $\angle \mathit{BKO}=90°$ ，

在 $\text{Rt}\Delta \text{BOK}$ 中， $\mathit{OB}=\mathit{OA}=6400$ ．

$\mathit{BK}=\mathit{OB}\times$ 　　（填" $\sin B$ "或" $\cos B$ " $)$ ．

所以北纬 $44°$ 的纬线长 $C=2\pi \cdot \mathit{BK}$ ．

$=2\times 3\times 6400\times$ 　　（填相应的三角形函数值）

$\approx$ 　　 $\left(\mathit{km}\right)$ （结果取整数）．

如图，在 $\mathit{\Delta ABC}$中， $\angle \mathit{ACB}=90°$， $\mathit{AC}=m$， $\mathit{BC}=n$， $m>n$，点 $P$是边 $\mathit{AB}$上一点，连接 $\mathit{CP}$，将 $\mathit{\Delta ACP}$沿 $\mathit{CP}$翻折得到 $\mathit{\Delta QCP}$．

（1）若 $m=4$， $n=3$，且 $\mathit{PQ}\perp \mathit{AB}$，求 $\mathit{BP}$的长；

（2）连接 $\mathit{BQ}$，若四边形 $\mathit{BCPQ}$是平行四边形，求 $m$与 $n$之间的关系式．

如图1，在平面直角坐标系中，直线 $\mathit{MN}$分别与 $x$轴、 $y$轴交于点 $M(6,0)$， $N(0$， $2\sqrt{3})$，等边 $\mathit{\Delta ABC}$的顶点 $B$与原点 $O$重合， $\mathit{BC}$边落在 $x$轴正半轴上，点 $A$恰好落在线段 $\mathit{MN}$上，将等边 $\mathit{\Delta ABC}$从图1的位置沿 $x$轴正方向以每秒1个单位长度的速度平移，边 $\mathit{AB}$， $\mathit{AC}$分别与线段 $\mathit{MN}$交于点 $E$， $F$（如图2所示），设 $\mathit{\Delta ABC}$平移的时间为 $t\left(s\right)$．

（1）等边 $\mathit{\Delta ABC}$的边长为　　；

（2）在运动过程中，当 $t=$　　时， $\mathit{MN}$垂直平分 $\mathit{AB}$；

（3）若在 $\mathit{\Delta ABC}$开始平移的同时．点 $P$从 $\mathit{\Delta ABC}$的顶点 $B$出发．以每秒2个单位长度的速度沿折线 $\mathit{BA}-\mathit{AC}$运动．当点 $P$运动到 $C$时即停止运动． $\mathit{\Delta ABC}$也随之停止平移．

①当点 $P$在线段 $\mathit{BA}$上运动时，若 $\mathit{\Delta PEF}$与 $\mathit{\Delta MNO}$相似．求 $t$的值；

②当点 $P$在线段 $\mathit{AC}$上运动时，设 $S_{\mathit{\Delta PEF}}=S$，求 $S$与 $t$的函数关系式，并求出 $S$的最大值及此时点 $P$的坐标．

在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{BC}$，点 $O$是 $\mathit{AC}$的中点，点 $P$是 $\mathit{AC}$上的一个动点（点 $P$不与点 $A$， $O$， $C$重合）．过点 $A$，点 $C$作直线 $\mathit{BP}$的垂线，垂足分别为点 $E$和点 $F$，连接 $\mathit{OE}$， $\mathit{OF}$．

（1）如图1，请直接写出线段 $\mathit{OE}$与 $\mathit{OF}$的数量关系；

（2）如图2，当 $\angle \mathit{ABC}=90°$时，请判断线段 $\mathit{OE}$与 $\mathit{OF}$之间的数量关系和位置关系，并说明理由

（3）若 $|\mathit{CF}-\mathit{AE}|=2$， $\mathit{EF}=2\sqrt{3}$，当 $\mathit{\Delta POF}$为等腰三角形时，请直接写出线段 $\mathit{OP}$的长．

如图，抛物线 $y=a{x}^2+\mathit{bx}-5(a\ne 0)$ 经过点 $A(4,-5)$ ，与 $x$ 轴的负半轴交于点 $B$ ，与 $y$ 轴交于点 $C$ ，且 $\mathit{OC}=5\mathit{OB}$ ，抛物线的顶点为点 $D$ ．

（1）求这条抛物线的表达式；

（2）联结 $\mathit{AB}$ 、 $\mathit{BC}$ 、 $\mathit{CD}$ 、 $\mathit{DA}$ ，求四边形 $\mathit{ABCD}$ 的面积；

（3）如果点 $E$ 在 $y$ 轴的正半轴上，且 $\angle \mathit{BEO}=\angle \mathit{ABC}$ ，求点 $E$ 的坐标．

如图，为⊙O的直径，是延长线上一点，切⊙O于点，是⊙O的弦，，垂足为．

（1）求证：；
（2）过点作交⊙O于点，交于点，连接．若，，求的长．