图①、②分别是某种型号跑步机的实物图与示意图，已知踏板CD长为1．6m，CD与地面DE的夹角∠CDE为12°，支架AC长为0．8m，∠ACD为80°，求跑步机手柄的一端A的高度h（精确到0．1m）．
（参考数据：sin12°=cos78°≈0．21，sin68°=cos22°≈0．93，tan68°≈2．48）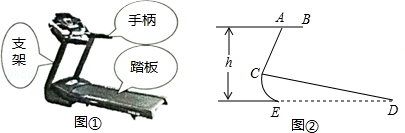
相关试题
；（2）
．
，其中
，
.
－3x＝x2－5x＋1.
，求所捂二次三项式的值.
·
，其中a＝－
．相关知识点
推荐套卷
图①、②分别是某种型号跑步机的实物图与示意图，已知踏板CD长为1．6m，CD与地面DE的夹角∠CDE为12°，支架AC长为0．8m，∠ACD为80°，求跑步机手柄的一端A的高度h（精确到0．1m）．
（参考数据：sin12°=cos78°≈0．21，sin68°=cos22°≈0．93，tan68°≈2．48）
粤公网安备 44130202000953号