上海市浦东新区第四教育署九年级上学期期中质量抽测数学试卷
如果两个相似三角形对应高之比是9∶16,那么它们的对应周长之比是 ( )
| A.3∶4 | B.4∶3 | C.9∶16 | D.16∶9 |
Rt△ABC中,∠C=90º,若AC=a,∠A= ,则AB的长为( )
,则AB的长为( )
A.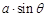 ; ; |
B.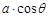 |
C.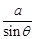 |
D.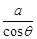 |
在比例尺为30∶1的图纸上,图上10cm的线段实际长为 ( )
| A.3cm | B.300cm | C.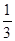 cm cm |
D.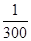 cm cm |
如图,能推得DE∥BC的条件是( )

| A.AD∶AB=DE∶BC |
| B.AD∶DB=DE∶BC |
| C.AE∶AC=AD∶DB |
| D.AD∶DB=AE∶EC |
如图,在Rt△ABC中,CD是斜边AB上的中线,如果CD=2,AC=3,那么sinB的值是( )

A. |
B. |
C. |
D. |
在△ABC中, 点D、E分别在边AB、AC上,如果DE//BC, AD:BD=2∶3, 那么DE:BC=_______________.
在△ABC中, 点D、E分别是边AB、AC的中点,那么SΔADE:S四边形DBCE= .
在△ABC中, 点D在AB上,如果∠ACD=∠B, AD=1, AB="4" , 那么AC=_________.
如果点G是△ABC的重心, AG的延长线交BC于点D, GD=12, 那么AG=________.
在△ABC中, 点D、E分别在边AB、AC上,要使 ,只须添加一个条件, 这个条件可以是:_____________________.(只要填写一种情况)
,只须添加一个条件, 这个条件可以是:_____________________.(只要填写一种情况)
在Rt△ABC中,∠C=90º,如果AB=10, AC=6,那么∠B的度数约为 (备用数据: )
)
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.在 Rt△ABC中,∠C=90°,若Rt△ABC是“好玩三角形”,则tanA= .
已知AD、BE是锐角△ABC的两条高,且AD、BE交于点H,若 ,则
,则 的值为_________.
的值为_________.
如图,已知两个不平行的向量 、
、 .先化简,再求作:2(
.先化简,再求作:2( +
+
 )-
)- (2
(2 -4
-4 )(不要求写作法,但要指出图中表示结论的向量)
)(不要求写作法,但要指出图中表示结论的向量)
小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论:如图,已知锐角△ABC,则

(1)试证明上述结论;
(2)运用这个新的结论,请完成下题:如图,在等腰△ABC中,AB=AC=12厘米,点P从A点出发,沿着边AB移动,点Q从C点出发沿着边CA移动,点Q的速度是1厘米/秒,点P的速度是点Q速度的2倍,若它们同时出发,设移动时间为t秒,问:当t为何值时, ?
?
已知:如图,在梯形ABCD中,AD//BC,∠BCD=90º,对角线AC、BD相交于点E,且AC⊥BD.
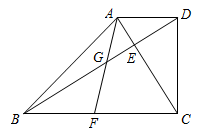
(1)求证: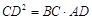 ;
;
(2)点F是边BC上一点,联结AF,与BD相交于点G.如果∠BAF =∠DBF,求证: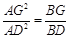 .
.
如图,在平面直角系中,直线 :
:
 分别交
分别交 轴、
轴、 轴于
轴于 、
、 两点,直线
两点,直线 分别交
分别交 轴、
轴、 轴于
轴于 、
、 两点,
两点, 是
是 轴上的一点,
轴上的一点, ,过
,过 作
作 轴交
轴交 于
于 ,连接
,连接 ,当动点
,当动点 在线段
在线段 上运动(不与点
上运动(不与点 点
点 重合)且
重合)且 时
时
(1)求证: ∽
∽ ;
;
(2)求线段 的长(用
的长(用 的代数式表示);
的代数式表示);
(3)若直线 的方程是
的方程是 ,求tan∠BAC的值.
,求tan∠BAC的值.

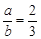 ,那么
,那么 .
. +
+ -3
-3 )-2(
)-2( -
-
 -
- 中,
中, ,
, ,
,  ,则
,则 .
. .
. 中,
中, 平分
平分 交
交 于点
于点 ,
, 交
交 于点
于点 ,
, ,
, ,
, .求
.求 与
与 的长.
的长.
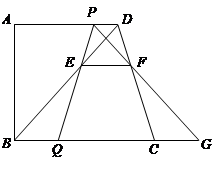
 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号