小华同学学习了第二十五章《锐角三角比》后，对求三角形的面积方法进行了研究，得到了新的结论：如图，已知锐角△ABC，则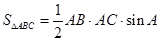
（1）试证明上述结论；
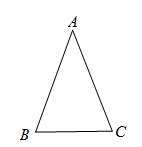
（2）运用这个新的结论，请完成下题：如图，在等腰△ABC中，AB=AC=12厘米，点P从A点出发，沿着边AB移动，点Q从C点出发沿着边CA移动，点Q的速度是1厘米/秒，点P的速度是点Q速度的2倍，若它们同时出发，设移动时间为t秒，问：当t为何值时，
?
相关试题
。
的面积。
并写出不等式组的整数解。
推荐套卷
小华同学学习了第二十五章《锐角三角比》后，对求三角形的面积方法进行了研究，得到了新的结论：如图，已知锐角△ABC，则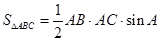
（1）试证明上述结论；
（2）运用这个新的结论，请完成下题：如图，在等腰△ABC中，AB=AC=12厘米，点P从A点出发，沿着边AB移动，点Q从C点出发沿着边CA移动，点Q的速度是1厘米/秒，点P的速度是点Q速度的2倍，若它们同时出发，设移动时间为t秒，问：当t为何值时，?
粤公网安备 44130202000953号