初中数学解直角三角形解答题

（本小题满分8分）如图，登山缆车从点A出发，途经点B后到达终点C，其中AB段与BC段的运行路程均为200m，且AB段的运行路线与水平面的夹角为30°，BC段的运行路线与水平面的夹角为42°，求缆车从点A运行到点C的垂直上升的距离．（参考数据：sin42°≈0.67 ，cos42°≈0.74 ， tan42°≈0.90）

如图，以 $\mathit{AB}$边为直径的 $\odot O$经过点 $P$， $C$是 $\odot O$上一点，连接 $\mathit{PC}$交 $\mathit{AB}$于点 $E$，且 $\angle \mathit{ACP}=60°$， $\mathit{PA}=\mathit{PD}$．

（1）试判断 $\mathit{PD}$与 $\odot O$的位置关系，并说明理由；

（2）若点 $C$是弧 $\mathit{AB}$的中点，已知 $\mathit{AB}=4$，求 $\mathit{CE}\cdot \mathit{CP}$的值．

某所学校位于北纬21°，此地一年中冬至日正午时刻，太阳光与地面的夹角最小，约为35．5°；夏至日正午时刻，太阳光的夹角最大，约为82．5°．己知该校一教学楼窗户朝南，窗高207cm，如图（1）．请你为该窗户设计一个直角形遮阳棚BCD，如图（2），要求最大限度地节省材料，夏至日正午刚好遮住全部阳光，冬至日正午能射入室内的阳光没有遮挡．

（1）在图（3）中画出设计草图；
（2）求BC、CD的长度（结果精确到个位）
（参考数据：sin35．5°≈0．58，cos35．5°≈0．81，tan35．5°≈0．71，sin82．5°≈0．99，cos82．5°≈0．13，tan82．5°≈7．60）

小敏同学测量一建筑物CD的高度，她站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走30m，到达点F处测得楼顶C的仰角为45°（BFD在同一直线上）．已知小敏的眼睛与地面距离为1．5m，求这栋建筑物CD的高度（参考数据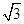：≈1．732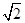，≈1．414．结果保留整数）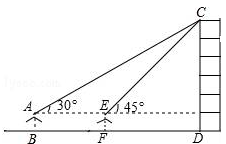

为了弘扬九十五中学办学理念，我校将“立己立人，尽善尽美”的校训印在旗帜上，放置在教学楼的顶部（如图所示）。小华在教学楼前空地上的点D处，用1米高的测角仪CD，从点C测得旗帜的底部B的仰角为37°，然后向教学楼正方向走了4．8米到达点F处，又从点E测得旗帜的顶部A的仰角为45°。若教学楼高BM=19米，且点A、B、M在同一直线上，求旗帜AB的高度（参考数据：sin37°≈0．60，cos37°≈0．81，tan37°≈0．75）

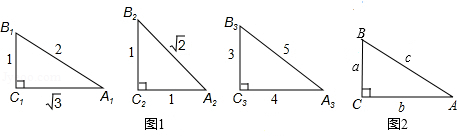
把 ${\left(\sin \alpha \right)}^2$记作 ${\sin }^2\alpha$，根据图1和图2完成下列各题．

（1） ${\sin }^2{A}_1+{\cos }^2{A}_1=$　　， ${\sin }^2{A}_2+{\cos }^2{A}_2=$　　， ${\sin }^2{A}_3+{\cos }^2{A}_3=$　　；

（2）观察上述等式猜想：在 $\text{Rt}\Delta \text{ABC}$中， $\angle C=90°$，总有 ${\sin }^{2}A+{\cos }^{2}A=$　　；

（3）如图2，在 $\text{Rt}\Delta \text{ABC}$中证明（2）题中的猜想：

（4）已知在 $\mathit{\Delta ABC}$中， $\angle A+\angle B=90°$，且 $\sin A=\frac{12}{13}$，求 $\cos A$．

如图，在 $▱\mathit{ABCD}$ 中， $E$ ， $F$ 是对角线 $\mathit{BD}$ 上的两点（点 $E$ 在点 $F$ 左侧），且 $\angle \mathit{AEB}=\angle \mathit{CFD}=90°$ ．

（1）求证：四边形 $\mathit{AECF}$ 是平行四边形；

（2）当 $\mathit{AB}=5$ ， $\tan \angle \mathit{ABE}=\frac{3}{4}$ ， $\angle \mathit{CBE}=\angle \mathit{EAF}$ 时，求 $\mathit{BD}$ 的长．

如图，已知 $\mathit{AB}$ 是 $\odot O$ 的直径， $\angle \mathit{ACD}$ 是 $\widehat{\mathit{AD}}$ 所对的圆周角， $\angle \mathit{ACD}=30°$ ．

（1）求 $\angle \mathit{DAB}$ 的度数；

（2）过点 $D$ 作 $\mathit{DE}\perp \mathit{AB}$ ，垂足为 $E$ ， $\mathit{DE}$ 的延长线交 $\odot O$ 于点 $F$ ．若 $\mathit{AB}=4$ ，求 $\mathit{DF}$ 的长．

如图，已知点 $C$ 是以 $\mathit{AB}$ 为直径的半圆上一点， $D$ 是 $\mathit{AB}$ 延长线上一点，过点 $D$ 作 $\mathit{BD}$ 的垂线交 $\mathit{AC}$ 的延长线于点 $E$ ，连结 $\mathit{CD}$ ，且 $\mathit{CD}=\mathit{ED}$ ．

（1）求证： $\mathit{CD}$ 是 $\odot O$ 的切线；

（2）若 $\tan \angle \mathit{DCE}=2$ ， $\mathit{BD}=1$ ，求 $\odot O$ 的半径．

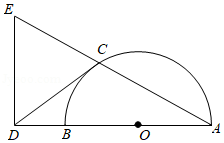
数学小组研究如下问题：长春市的纬度约为北纬 $44°$ ，求北纬 $44°$ 纬线的长度，小组成员查阅了相关资料，得到三条信息：

（1）在地球仪上，与南，北极距离相等的大圆圈，叫赤道，所有与赤道平行的圆圈叫纬线；

（2）如图， $\odot O$ 是经过南、北极的圆，地球半径 $\mathit{OA}$ 约为 $6400\mathit{km}$ ．弦 $\mathit{BC}//\mathit{OA}$ ，过点 $O$ 作 $\mathit{OK}\perp \mathit{BC}$ 于点 $K$ ，连接 $\mathit{OB}$ ．若 $\angle \mathit{AOB}=44°$ ，则以 $\mathit{BK}$ 为半径的圆的周长是北纬 $44°$ 纬线的长度；

（3）参考数据： $\pi$ 取3， $\sin 44°=0.69$ ， $\cos 44°=0.72$ ．

小组成员给出了如下解答，请你补充完整：

解：因为 $\mathit{BC}//\mathit{OA}$ ， $\angle \mathit{AOB}=44°$ ，

所以 $\angle B=\angle \mathit{AOB}=44°($ 　　 $)$ （填推理依据），

因为 $\mathit{OK}\perp \mathit{BC}$ ，所以 $\angle \mathit{BKO}=90°$ ，

在 $\text{Rt}\Delta \text{BOK}$ 中， $\mathit{OB}=\mathit{OA}=6400$ ．

$\mathit{BK}=\mathit{OB}\times$ 　　（填" $\sin B$ "或" $\cos B$ " $)$ ．

所以北纬 $44°$ 的纬线长 $C=2\pi \cdot \mathit{BK}$ ．

$=2\times 3\times 6400\times$ 　　（填相应的三角形函数值）

$\approx$ 　　 $\left(\mathit{km}\right)$ （结果取整数）．

如图，在 $\mathit{\Delta ABC}$中， $\angle \mathit{ACB}=90°$， $\mathit{AC}=m$， $\mathit{BC}=n$， $m>n$，点 $P$是边 $\mathit{AB}$上一点，连接 $\mathit{CP}$，将 $\mathit{\Delta ACP}$沿 $\mathit{CP}$翻折得到 $\mathit{\Delta QCP}$．

（1）若 $m=4$， $n=3$，且 $\mathit{PQ}\perp \mathit{AB}$，求 $\mathit{BP}$的长；

（2）连接 $\mathit{BQ}$，若四边形 $\mathit{BCPQ}$是平行四边形，求 $m$与 $n$之间的关系式．

如图1，在平面直角坐标系中，直线 $\mathit{MN}$分别与 $x$轴、 $y$轴交于点 $M(6,0)$， $N(0$， $2\sqrt{3})$，等边 $\mathit{\Delta ABC}$的顶点 $B$与原点 $O$重合， $\mathit{BC}$边落在 $x$轴正半轴上，点 $A$恰好落在线段 $\mathit{MN}$上，将等边 $\mathit{\Delta ABC}$从图1的位置沿 $x$轴正方向以每秒1个单位长度的速度平移，边 $\mathit{AB}$， $\mathit{AC}$分别与线段 $\mathit{MN}$交于点 $E$， $F$（如图2所示），设 $\mathit{\Delta ABC}$平移的时间为 $t\left(s\right)$．

（1）等边 $\mathit{\Delta ABC}$的边长为　　；

（2）在运动过程中，当 $t=$　　时， $\mathit{MN}$垂直平分 $\mathit{AB}$；

（3）若在 $\mathit{\Delta ABC}$开始平移的同时．点 $P$从 $\mathit{\Delta ABC}$的顶点 $B$出发．以每秒2个单位长度的速度沿折线 $\mathit{BA}-\mathit{AC}$运动．当点 $P$运动到 $C$时即停止运动． $\mathit{\Delta ABC}$也随之停止平移．

①当点 $P$在线段 $\mathit{BA}$上运动时，若 $\mathit{\Delta PEF}$与 $\mathit{\Delta MNO}$相似．求 $t$的值；

②当点 $P$在线段 $\mathit{AC}$上运动时，设 $S_{\mathit{\Delta PEF}}=S$，求 $S$与 $t$的函数关系式，并求出 $S$的最大值及此时点 $P$的坐标．

在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{BC}$，点 $O$是 $\mathit{AC}$的中点，点 $P$是 $\mathit{AC}$上的一个动点（点 $P$不与点 $A$， $O$， $C$重合）．过点 $A$，点 $C$作直线 $\mathit{BP}$的垂线，垂足分别为点 $E$和点 $F$，连接 $\mathit{OE}$， $\mathit{OF}$．

（1）如图1，请直接写出线段 $\mathit{OE}$与 $\mathit{OF}$的数量关系；

（2）如图2，当 $\angle \mathit{ABC}=90°$时，请判断线段 $\mathit{OE}$与 $\mathit{OF}$之间的数量关系和位置关系，并说明理由

（3）若 $|\mathit{CF}-\mathit{AE}|=2$， $\mathit{EF}=2\sqrt{3}$，当 $\mathit{\Delta POF}$为等腰三角形时，请直接写出线段 $\mathit{OP}$的长．

如图，抛物线 $y=a{x}^2+\mathit{bx}-5(a\ne 0)$ 经过点 $A(4,-5)$ ，与 $x$ 轴的负半轴交于点 $B$ ，与 $y$ 轴交于点 $C$ ，且 $\mathit{OC}=5\mathit{OB}$ ，抛物线的顶点为点 $D$ ．

（1）求这条抛物线的表达式；

（2）联结 $\mathit{AB}$ 、 $\mathit{BC}$ 、 $\mathit{CD}$ 、 $\mathit{DA}$ ，求四边形 $\mathit{ABCD}$ 的面积；

（3）如果点 $E$ 在 $y$ 轴的正半轴上，且 $\angle \mathit{BEO}=\angle \mathit{ABC}$ ，求点 $E$ 的坐标．

如图，为⊙O的直径，是延长线上一点，切⊙O于点，是⊙O的弦，，垂足为．

（1）求证：；
（2）过点作交⊙O于点，交于点，连接．若，，求的长．