广西梧州市初中毕业升学考试抽样调研测试一数学试卷
已知⊙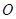 的半径为
的半径为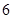
 ,圆心
,圆心 到直线
到直线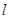 的距离为
的距离为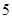
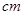 ,则直线
,则直线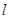 与⊙
与⊙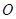 的交点个数为( )
的交点个数为( )
A. |
B.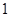 |
C.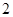 |
D.无法确定 |
如图,一张矩形纸片 的长
的长 ,宽
,宽 .将纸片对折,折痕为
.将纸片对折,折痕为 ,所得矩形
,所得矩形 与矩形
与矩形 相似,则
相似,则 ( )
( )
A. |
B. |
C. |
D. |
如图,半圆 的直径为
的直径为 ,
, ,
, 为
为 的三等分点.
的三等分点. 交半圆于
交半圆于 ,
, ,且
,且 ,
, ,则它的半径是( )
,则它的半径是( )
A. |
B. |
C. |
D. |
如图,菱形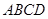 的一个内角是
的一个内角是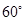 ,将它绕对角线的交点
,将它绕对角线的交点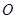 顺时针旋转
顺时针旋转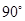 后得到菱形
后得到菱形 .旋转前后两菱形重叠部分多边形的周长为
.旋转前后两菱形重叠部分多边形的周长为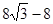 ,则菱形
,则菱形 的边长为 .
的边长为 .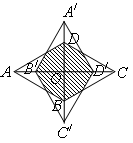
春节过后,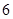 名村民用
名村民用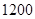 元共同租用一辆小客车去广东工作.出发时又增加部分村民,结果每位村民比原来少分摊
元共同租用一辆小客车去广东工作.出发时又增加部分村民,结果每位村民比原来少分摊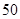 元.求增加村民的人数.
元.求增加村民的人数.
某市记者为了调查该市市民对雾霾天气成因的认识情况,进行了随机调查,并对结果绘制成如下不完整的统计图表.
| 组别 |
观点 |
频数 |
| A |
大气气压低,空气不流动 |
 |
| B |
地面灰尘大,空气湿度低 |
 |
| C |
汽车尾气排放 |
 |
| D |
工厂造成的污染 |
 |
| E |
其他 |
 |
请根据图表中提供的信息解答下列问题:
(1) ,
,
 ;
;
(2)若该市人口约为 万人,请你估计其中持
万人,请你估计其中持 组“观点”的市民人数;
组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,抽中持 组“观点”的人概率是多少?
组“观点”的人概率是多少?
如图,某校一大楼 的高为
的高为 米,不远处有一水塔
米,不远处有一水塔 .某同学在楼底
.某同学在楼底 处测得塔顶
处测得塔顶 处的仰角为
处的仰角为 ,在楼顶
,在楼顶 点测得塔顶
点测得塔顶 处的仰角为
处的仰角为 .求
.求 的高度(结果精确到
的高度(结果精确到 米) .(参考数据:
米) .(参考数据: ,
, ,
, ,
, ,
, ,)
,)
为迎接2014年世界杯足球赛,某商家购进甲、乙两种纪念品.甲种纪念品的进货价 (元/件)与进货数量
(元/件)与进货数量 (件)的关系如图所示.
(件)的关系如图所示. 
(1)求 与
与 的关系式;
的关系式;
(2)若商家购进甲种纪念品的数量 不少于
不少于 件,且甲种纪念品的进货价不低于
件,且甲种纪念品的进货价不低于 元/件,则该商家有几种进货方案?
元/件,则该商家有几种进货方案?
(3)该商家若购进甲、乙两种纪念品共 件,其中乙种纪念品的进货价
件,其中乙种纪念品的进货价 (元/件)与进货数量
(元/件)与进货数量 (件)满足关系式
(件)满足关系式 .商家分别以
.商家分别以 元/件、
元/件、 元/件出售甲、乙两种纪念品,并且全部售完.在(2)的条件下,购进甲种纪念品多少件时,所获总利润最大?最大利润是多少?(说明:本题不要求写出自变量
元/件出售甲、乙两种纪念品,并且全部售完.在(2)的条件下,购进甲种纪念品多少件时,所获总利润最大?最大利润是多少?(说明:本题不要求写出自变量 的取值范围)
的取值范围)
如图,已知 、
、 是⊙
是⊙ 的切线,
的切线, 、
、 为切点.直径
为切点.直径 的延长线与
的延长线与 的延长线交于点
的延长线交于点 .
.
(1)求证: ;
;
(2)若 ,
, .求图中阴影部分的面积(结果保留根号与
.求图中阴影部分的面积(结果保留根号与 ).
).
 的倒数是( )
的倒数是( )
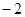
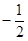




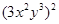 结果正确的是( )
结果正确的是( )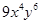
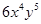
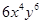
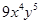
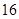 ,底边长是
,底边长是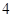 ,则它的腰长是( )
,则它的腰长是( )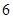
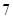
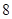
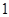 ,
,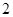 ,
,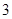 ,
,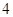 ,
,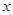 ,若它们的众数是
,若它们的众数是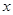 ,
,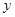 满足
满足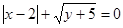 ,则
,则 的值是( )
的值是( )
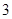
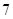
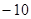
 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )



 ,则这个多边形的边数是( )
,则这个多边形的边数是( )



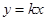
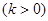 与双曲线
与双曲线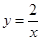 交于
交于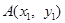 、
、 两点,则
两点,则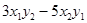 的值是( )
的值是( )
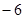
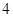

 .
.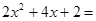 .
. 、
、 被直线
被直线 所截.若
所截.若 ,
, ,
, ,则
,则 度.
度.
 ,
, 的方程组
的方程组 中,
中, .
. 中,点
中,点 、
、 、
、 分别为
分别为 、
、 、
、 的中点.若
的中点.若 ,则
,则 .
.
 .
. 的对角线
的对角线 、
、 交于点
交于点 ,
, 过点
过点 、
、 交于点
交于点 、
、 .求证:
.求证: .
.
 经过
经过 两点.连结
两点.连结 ,过点
,过点 作
作 ,交抛物线于点
,交抛物线于点 .
.
 的坐标;
的坐标; 轴的直线对折,再向上平移到某个位置后此抛物线与直线
轴的直线对折,再向上平移到某个位置后此抛物线与直线 粤公网安备 44130202000953号
粤公网安备 44130202000953号