初中数学解直角三角形计算题

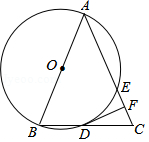
如图，在△ABC中，点D在AC上，DA=DB，∠C=∠DBC，以AB为直径的交AC于点E，F是上的点，且AF＝BF．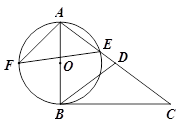

（1）求证：BC是的切线；
（2）若sinC=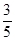，AE=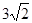，求sinF的值和AF的长．

如图①，菱形 $\mathit{ABCD}$中， $\mathit{AB}=5\mathit{cm}$，动点 $P$从点 $B$出发，沿折线 $\mathit{BC}-\mathit{CD}-\mathit{DA}$运动到点 $A$停止，动点 $Q$从点 $A$出发，沿线段 $\mathit{AB}$运动到点 $B$停止，它们运动的速度相同，设点 $P$出发 $\mathit{xs}$时， $\mathit{\Delta BPQ}$的面积为 $\mathit{yc}{m}^2$．已知 $y$与 $x$之间的函数关系如图②所示，其中 $\mathit{OM}$、 $\mathit{MN}$为线段，曲线 $\mathit{NK}$为抛物线的一部分．请根据图中的信息，解答下列问题：

（1）当 $1<x<2$时， $\mathit{\Delta BPQ}$的面积　    　（填“变”或“不变” $)$；

（2）分别求出线段 $\mathit{OM}$，曲线 $\mathit{NK}$所对应的函数表达式；

（3）当 $x$为何值时， $\mathit{\Delta BPQ}$的面积是 $5c{m}^2$？

如图，小山的顶部是平地，在这块平地上有一高压输电线架，小山的斜坡BD的坡度i=1﹕，长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°，在山坡的坡顶D处测得铁架顶端A的仰角为60°。

求： ①小山的高度CE。
②铁架的高度AE。（≈1.73，精确到0.1米）。

如图是某宾馆大厅到二楼的楼梯设计图，已知米，米，为平台的两根支柱，垂直于，垂足分别为，，．

（1）若中间平台高度为3米，求中间平台宽度的长．（结果保留根号）
（2）若中间平台宽度为2米，求和之间的水平距离的长．（结果保留整米数，参考数据：≈1．4，≈1．7）

（本题6分）
（1）已知：sinα·cos60°＝,求锐角α.
（2）计算：.

计算：2sin60°＋cos60°－3tan30°．

如图，在△ABC中，∠ABC=90°，以AB的中点O为圆心，OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE．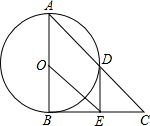

（1）判断DE与⊙O的位置关系，并说明理由；
（2）若cos∠BAD=，BE=，求OE的长．

计算：
（1）sin30°－cos45°+tan²60°
（2）

如图，在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$，以 $\mathit{AB}$为直径的 $\odot O$与边 $\mathit{BC}$、 $\mathit{AC}$分别交于 $D$、 $E$两点，过点 $D$作 $\mathit{DF}\perp \mathit{AC}$，垂足为点 $F$．

（1）求证： $\mathit{DF}$是 $\odot O$的切线；

（2）若 $\mathit{AE}=4$， $\cos A=\frac{2}{5}$，求 $\mathit{DF}$的长．

如图，已知 $\mathit{AC}\perp \mathit{BC}$，垂足为 $C$， $\mathit{AC}=4$， $\mathit{BC}=3\sqrt{3}$，将线段 $\mathit{AC}$绕点 $A$按逆时针方向旋转 $60°$，得到线段 $\mathit{AD}$，连接 $\mathit{DC}$， $\mathit{DB}$．

（1）线段 $\mathit{DC}=$　     　；

（2）求线段 $\mathit{DB}$的长度．

（本题8分）计算：
（1）
（2）

计算：（1）．
（2）已知是锐角，且计算

计算：
（1）
（2）．

如图1，以 $\mathit{\Delta ABC}$的边 $\mathit{AB}$为直径的 $\odot O$交边 $\mathit{BC}$于点 $E$，过点 $E$作 $\odot O$的切线交 $\mathit{AC}$于点 $D$，且 $\mathit{ED}\perp \mathit{AC}$．

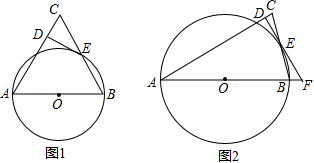
（1）试判断 $\mathit{\Delta ABC}$的形状，并说明理由；

（2）如图2，若线段 $\mathit{AB}$、 $\mathit{DE}$的延长线交于点 $F$， $\angle C=75°$， $\mathit{CD}=2-\sqrt{3}$，求 $\odot O$的半径和 $\mathit{BF}$的长．

（本小题满分8分）某市地铁工程正在加快建设，为了缓解市区内一些主要路段交通拥挤的现状，交警大队在一些主要路口设立了交通路况指示牌，如图所示，小明在离指示牌3．2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和30°．求路况指示牌DE的高度．（精确到0．01米，参考数据：≈1．732，sin52°≈0．79，cos52°≈0．62, tan52°≈1．28．）