已知等边三角形 ,过 点作 的垂线 ,点 为 上一动点(不与点 重合),连接 ,把线段 绕点 逆时针方向旋转 得到 ,连 .
(1)如图1,直接写出线段 与 的数量关系;
(2)如图2,当点 、 在 同侧且 时,求证:直线 垂直平分线段 ;
(3)如图3,若等边三角形 的边长为4,点 、 分别位于直线 异侧,且 的面积等于 ,求线段 的长度.

如图,已知 是 的直径. 是 的弦,弦 垂直 于点 ,交 于点 .过点 作 的切线交 的延长线于点
(1)求证: ;
(2)判断 是否成立?若成立,请证明该结论;
(3)若 为 中点, , ,求 的长.
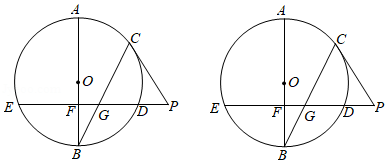
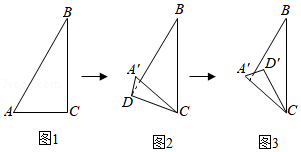
小华用一张直角三角形纸片玩折纸游戏,如图1,在 中, , , .第一步,在 边上找一点 ,将纸片沿 折叠,点 落在 处,如图2;第二步,将纸片沿 折叠,点 落在 处,如图3.当点 恰好落在原直角三角形纸片的边上时,线段 的长为 .
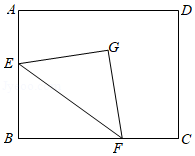
在四边形 中,对角线 平分 .
【探究发现】
(1)如图①,若 , .求证: ;
【拓展迁移】
(2)如图②,若 , .
①猜想 、 、 三条线段的数量关系,并说明理由;
②若 ,求四边形 的面积.

如图,在 中, 为 的直径, 为 的弦,点 是 的中点,过点 作 的垂线,交 于点 ,交 于点 ,分别连接 , .
(1) 与 的数量关系是 ;
(2)求证: ;
(3)若 , ,求阴影部分图形的面积.

如图,在正六边形 中,连接对角线 , , , , , 与 交于点 , 与 交于点为 , 与 交于点 ,分别延长 , 于点 ,设 .有以下结论:
①
②
③ 的重心、内心及外心均是点
④四边形 绕点 逆时针旋转 与四边形 重合
则所有正确结论的序号是 .

如图,在 中, , 是 上的一点,以 为直径的 与 相切于点 ,连接 , .
(1)求证: 平分 ;
(2)若 ,求 的值.

如图.在边长为6的正方形 中,点 , 分别在 , 上, 且 , ,垂足为 , 是对角线 的中点,连接 、则 的长为 .

如图,在四边形 中, , , ,点 、 分别在线段 、 上,且 , , .
(1)求证: ;
(2)求证:以 为直径的圆与 相切;
(3)若 , ,求 的面积.
如图,在矩形 中, , ,点 , 分别是边 , 上的动点,点 不与 , 重合,且 , 是五边形 内满足 且 的点.现给出以下结论:
① 与 一定互补;
②点 到边 , 的距离一定相等;
③点 到边 , 的距离可能相等;
④点 到边 的距离的最大值为 .
其中正确的是 .(写出所有正确结论的序号)
如图,在四边形 中, ,点 在 上, , ,垂足为 .
(1)求证:四边形 是平行四边形;
(2)若 平分 , , ,求 和 的长.
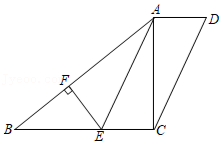
△ABC为等边三角形, , 于点D,E为线段 上一点, .以AE为边在直线 右侧构造等边三角形 ,连接 ,N为 的中点.
(1)如图1, 交于点G,连接 ,求线段 的长;
(2)如图2,将 绕点A逆时针旋转,旋转角为α,M为线段EF的中点,连接 , .当 时,猜想∠DNM的大小是否为定值,并证明你的结论;
(3)连接BN,在 绕点A逆时针旋转过程中,当线段BN最大时,请直接写出 的面积.

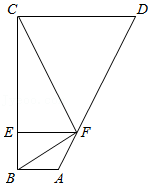
如图1,矩形 中, , , 中, , , , 的延长线相交于点 ,且 , , .将 绕点 逆时针旋转 得到△ .
(1)当 时,求点 到直线 的距离.
(2)在图1中,取 的中点 ,连结 ,如图2.
①当 与矩形 的一条边平行时,求点 到直线 的距离.
②当线段 与矩形 的边有且只有一个交点时,求该交点到直线 的距离的取值范围.
