初中数学相似三角形的判定与性质试题

如图，是的直径，、两点在的延长线上，是上的点，且，延长至，使得，设，．

（1）求证：；

（2）求，的长；

（3）若点在、、三点确定的圆上，求的长．

如图1，在矩形中，为边上一点，．将沿翻折得到△，的延长线交边于点，过点作交于点．

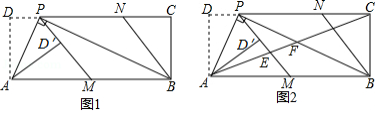
（1）求证：；

（2）请判断四边形的形状，并说明理由；

（3）如图2，连接，分别交，于点，．若，求的值．

已知是的直径，是的切线，是上的点，，是直径上的动点，与直线上的点连线距离的最小值为，与直线上的点连线距离的最小值为．

（1）求证：是的切线；

（2）设，求的正弦值；

（3）设，，求的取值范围．

如图，已知的半径长为1，、是的两条弦，且，的延长线交于点，联结、．

（1）求证：；

（2）当是直角三角形时，求、两点的距离；

（3）记、、 的面积分别为、、，如果是和的比例中项，求的长．

如图所示，梯形 $\mathit{ABCD}$ 中， $\mathit{AB}//\mathit{DC}$ ， $\angle B=90°$ ， $\mathit{AD}=15$ ， $\mathit{AB}=16$ ， $\mathit{BC}=12$ ，点 $E$ 是边 $\mathit{AB}$ 上的动点，点 $F$ 是射线 $\mathit{CD}$ 上一点，射线 $\mathit{ED}$ 和射线 $\mathit{AF}$ 交于点 $G$ ，且 $\angle \mathit{AGE}=\angle \mathit{DAB}$ ．

（1）求线段 $\mathit{CD}$ 的长；

（2）如果 $\mathit{\Delta AEG}$ 是以 $\mathit{EG}$ 为腰的等腰三角形，求线段 $\mathit{AE}$ 的长；

（3）如果点 $F$ 在边 $\mathit{CD}$ 上（不与点 $C$ 、 $D$ 重合），设 $\mathit{AE}=x$ ， $\mathit{DF}=y$ ，求 $y$ 关于 $x$ 的函数解析式，并写出 $x$ 的取值范围．

问题提出

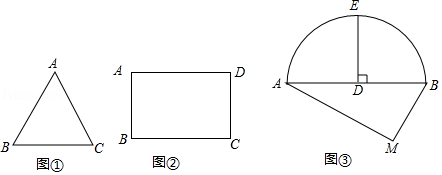
（1）如图①，是等边三角形，，若点是的内心，则的长为　　；

问题探究

（2）如图②，在矩形中，，，如果点是边上一点，且，那么边上是否存在一点，使得线段将矩形的面积平分？若存在，求出的长；若不存在，请说明理由．

问题解决

（3）某城市街角有一草坪，草坪是由草地和弦与其所对的劣弧围成的草地组成，如图③所示．管理员王师傅在处的水管上安装了一喷灌龙头，以后，他想只用喷灌龙头来给这块草坪浇水，并且在用喷灌龙头浇水时，既要能确保草坪的每个角落都能浇上水，又能节约用水，于是，他让喷灌龙头的转角正好等于（即每次喷灌时喷灌龙头由转到，然后再转回，这样往复喷灌．同时，再合理设计好喷灌龙头喷水的射程就可以了．

如图③，已测出，，的面积为；过弦的中点作交于点，又测得．

请你根据以上信息，帮助王师傅计算喷灌龙头的射程至少多少米时，才能实现他的想法？为什么？（结果保留根号或精确到0.01米）

如图，抛物线交轴于，两点，交轴于点．直线经过点，．

（1）求抛物线的解析式；

（2）点是抛物线上一动点，过点作轴的垂线，交直线于点，设点的横坐标为．

①当是直角三角形时，求点的坐标；

②作点关于点的对称点，则平面内存在直线，使点，，到该直线的距离都相等．当点在轴右侧的抛物线上，且与点不重合时，请直接写出直线的解析式．，可用含的式子表示）

如图，抛物线交轴于、两点，交轴于点，顶点的坐标为，对称轴交轴于点，直线交轴于点，交轴于点，交抛物线的对称轴于点．

（1）求出，，的值．

（2）点为抛物线对称轴上一个动点，若是以为腰的等腰三角形时，请求出点的坐标．

（3）点为抛物线上一个动点，当点关于直线的对称点恰好落在轴上时，请直接写出此时点的坐标．

如图，直线与轴交于点，与轴交于点，抛物线经过点，．

（1）求点的坐标和抛物线的解析式；

（2）为轴上一动点，过点且垂直于轴的直线与直线及抛物线分别交于点，．

①点在线段上运动，若以，，为顶点的三角形与相似，求点的坐标；

②点在轴上自由运动，若三个点，，中恰有一点是其它两点所连线段的中点（三点重合除外），则称，，三点为“共谐点”．请直接写出使得，，三点成为“共谐点”的的值．

如图，在平面直角坐标系中，有抛物线．抛物线经过原点，与轴正半轴交于点，与其对称轴交于点，是抛物线上一点，且在轴上方，过点作轴的垂线交抛物线于点，过点作的垂线交抛物线于点（不与点重合），连结，设点的横坐标为．

（1）求的值；

（2）当抛物线经过原点时，设与重叠部分图形的周长为．

①求的值；

②求与之间的函数关系式；

（3）当为何值时，存在点，使以点，，，为顶点的四边形是轴对称图形？直接写出的值．

如图1和图2，在中，，，．点在边上，点，分别在，上，且．点从点出发沿折线匀速移动，到达点时停止；而点在边上随移动，且始终保持．

（1）当点在上时，求点与点的最短距离；

（2）若点在上，且将的面积分成上下两部分时，求的长；

（3）设点移动的路程为，当及时，分别求点到直线的距离（用含的式子表示）；

（4）在点处设计并安装一扫描器，按定角扫描区域（含边界），扫描器随点从到再到共用时36秒．若，请直接写出点被扫描到的总时长．

如图，中，，，为内部一点，且．

（1）求证：；

（2）求证：；

（3）若点到三角形的边，，的距离分别为，，，求证．

已知正方形，点为边的中点．

（1）如图1，点为线段上的一点，且，延长、分别与边、交于点、．

①求证：；

②求证：．

（2）如图2，在边上取一点，满足，连接交于点，连接并延长交于点，求的值．

如图1，，分别在射线，上，且为钝角，现以线段，为斜边向的外侧作等腰直角三角形，分别是，，点，，分别是，，的中点．

（1）求证：；

（2）延长，交于点．

①如图2，若，求证：为等边三角形；

②如图3，若，求大小和的值．

如图，已知∠MON=90°，A是∠MON内部的一点，过点A作AB⊥ON，垂足为点B，AB=3厘米，OB=4厘米，动点E，F同时从O点出发，点E以1．5厘米/秒的速度沿ON方向运动，点F以2厘米/秒的速度沿OM方向运动，EF与OA交于点C，连接AE，当点E到达点B时，点F随之停止运动．设运动时间为t秒（t＞0）．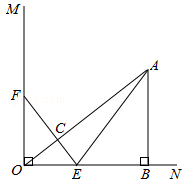

（1）当t=1秒时，△EOF与△ABO是否相似？请说明理由；
（2）在运动过程中，不论t取何值时，总有EF⊥OA．为什么？
（3）连接AF，在运动过程中，是否存在某一时刻t，使得S_△AEF=S_{四边形ABOF}？若存在，请求出此时t的值；若不存在，请说明理由．