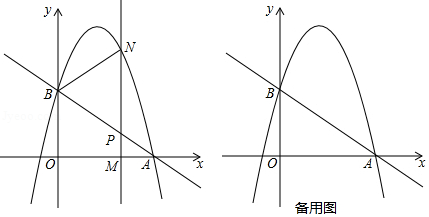
如图,直线与轴交于点,与轴交于点,抛物线经过点,.
(1)求点的坐标和抛物线的解析式;
(2)为轴上一动点,过点且垂直于轴的直线与直线及抛物线分别交于点,.
①点在线段上运动,若以,,为顶点的三角形与相似,求点的坐标;
②点在轴上自由运动,若三个点,,中恰有一点是其它两点所连线段的中点(三点重合除外),则称,,三点为“共谐点”.请直接写出使得,,三点成为“共谐点”的的值.
推荐套卷
如图,直线与轴交于点,与轴交于点,抛物线经过点,.
(1)求点的坐标和抛物线的解析式;
(2)为轴上一动点,过点且垂直于轴的直线与直线及抛物线分别交于点,.
①点在线段上运动,若以,,为顶点的三角形与相似,求点的坐标;
②点在轴上自由运动,若三个点,,中恰有一点是其它两点所连线段的中点(三点重合除外),则称,,三点为“共谐点”.请直接写出使得,,三点成为“共谐点”的的值.
