初中数学相似三角形的判定与性质试题

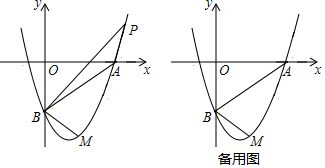
如图，在中，是斜边的中点，以为直径作圆交于点，延长至，使，连接、，交圆于点．

（1）判断四边形的形状，并说明理由；

（2）求证：；

（3）若，，求的长．

如图，内接于，，是的直径，与相交于点，过点作，分别交、的延长线于点、，连接．

（1）求证：是的切线；

（2）求证：．

如图，点在以为直径的上，平分，，过点作的切线交的延长线于点．

（1）求证：直线是的切线．

（2）求证：．

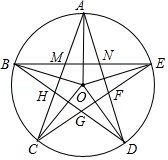
如图，、、、、是上的5等分点，连接、、、、，得到一个五角星图形和五边形．

（1）计算的度数；

（2）连接，证明：；

（3）求证：．

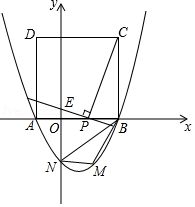
如图，二次函数的图象与轴交于点和点，与轴交于点，以为边在轴上方作正方形，点是轴上一动点，连接，过点作的垂线与轴交于点．

（1）求该抛物线的函数关系表达式；

（2）当点在线段（点不与、重合）上运动至何处时，线段的长有最大值？并求出这个最大值；

（3）在第四象限的抛物线上任取一点，连接、．请问：的面积是否存在最大值？若存在，求出此时点的坐标；若不存在，请说明理由．

如图1，矩形中，点为边上的动点（不与，重合），把沿翻折，点的对应点为，延长交直线于点，再把折叠，使点的对应点落在上，折痕交直线于点．

（1）求证：△△；

（2）如图2，直线是矩形的对称轴，若点恰好落在直线上，试判断的形状，并说明理由；

（3）如图3，在（2）的条件下，点为内一点，且，试探究，，的数量关系．

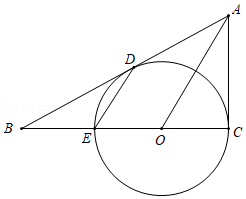
如图，与的边相切于点，与、边分别交于点、，，是的直径．

（1）求证：是的切线；

（2）若，，求的长．

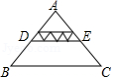
如图，在等腰三角形 $\mathit{\Delta ABC}$ 中， $\mathit{AB}=\mathit{AC}$ ，图中所有三角形均相似，其中最小的三角形面积为1， $\mathit{\Delta ABC}$ 的面积为42，则四边形 $\mathit{DBCE}$ 的面积是 $($ 　　 $)$

A．

20

B．

22

C．

24

D．

26

如图，在 $\mathit{\Delta ABC}$ 中， $\mathit{AC}=2$ ， $\mathit{BC}=4$ ， $D$ 为 $\mathit{BC}$ 边上的一点，且 $\angle \mathit{CAD}=\angle B$ ．若 $\mathit{\Delta ADC}$ 的面积为 $a$ ，则 $\mathit{\Delta ABD}$ 的面积为 $($ 　　 $)$

A．

$2a$

B．

$\frac{5}{2}a$

C．

$3a$

D．

$\frac{7}{2}a$

如图，将 $\mathit{\Delta ABC}$ 沿 $\mathit{BC}$ 边上的中线 $\mathit{AD}$ 平移到△ $A\text{'}B\text{'}C\text{'}$ 的位置．已知 $\mathit{\Delta ABC}$ 的面积为16，阴影部分三角形的面积9．若 $\mathit{AA}\text{'}=1$ ，则 $A\text{'}D$ 等于 $($ 　　 $)$

A．

2

B．

3

C．

4

D．

$\frac{3}{2}$

[问题探究]

（1）如图1，和均为等腰直角三角形，，点，，在同一直线上，连接，．

①请探究与之间的位置关系：　　；

②若，，则线段的长为　　；

[拓展延伸]

（2）如图2，和均为直角三角形，，，，，．将绕点在平面内顺时针旋转，设旋转角为，作直线，连接，当点，，在同一直线上时，画出图形，并求线段的长．

如图，中，，顶点，分别在反比例函数与的图象上，则的值为　　．

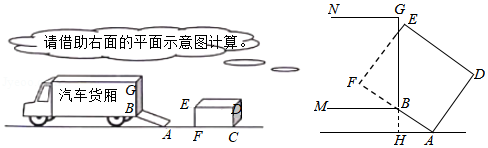
如图是把一个装有货物的长方体形状的木箱沿着坡面装进汽车货厢的示意图．已知汽车货厢高度米，货厢底面距地面的高度米，坡面与地面的夹角，木箱的长为2米，高和宽都是1.6米．通过计算判断：当，木箱底部顶点与坡面底部点重合时，木箱上部顶点会不会触碰到汽车货厢顶部．

若二次函数的图象与轴、轴分别交于点、，且过点．

（1）求二次函数表达式；

（2）若点为抛物线上第一象限内的点，且，求点的坐标；

（3）在抛物线上下方）是否存在点，使？若存在，求出点到轴的距离；若不存在，请说明理由．

在矩形中，于点，点是边上一点．

（1）若平分，交于点，于点，如图①，证明四边形是菱形；

（2）若，如图②，求证：；

（3）在（2）的条件下，若，，求的长．