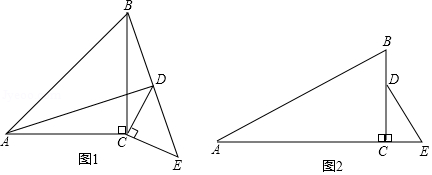
[问题探究]
(1)如图1,和均为等腰直角三角形,,点,,在同一直线上,连接,.
①请探究与之间的位置关系: ;
②若,,则线段的长为 ;
[拓展延伸]
(2)如图2,和均为直角三角形,,,,,.将绕点在平面内顺时针旋转,设旋转角为,作直线,连接,当点,,在同一直线上时,画出图形,并求线段的长.
推荐套卷
[问题探究]
(1)如图1,和均为等腰直角三角形,,点,,在同一直线上,连接,.
①请探究与之间的位置关系: ;
②若,,则线段的长为 ;
[拓展延伸]
(2)如图2,和均为直角三角形,,,,,.将绕点在平面内顺时针旋转,设旋转角为,作直线,连接,当点,,在同一直线上时,画出图形,并求线段的长.
