初中数学坐标与图形变化-旋转解答题

如图，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D、E两点的坐标．

在平面直角坐标系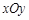中，对于任意三点、、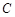的“矩面积”，给出如下定义：“水平底”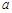：任意两点横坐标差的最大值，“铅垂高”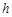：任意两点纵坐标差的最大值，则“矩面积”．
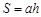例如：三点坐标分别为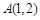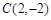，，，则“水平底”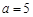，“铅垂高”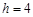，“矩面积”．
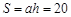（1）已知点，，．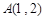
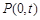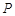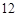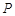①若、、三点的“矩面积”为，求点的坐标；
②、、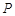三点的“矩面积”的最小值为         
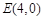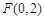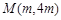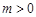（2）已知点，，，其中．若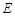、、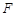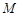三点的“矩面积”的为8，求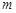的取值范围；

这是某单位的平面示意图，已知大门的坐标为（﹣3，0），花坛的坐标为（0，﹣1）．

（1）根据上述条件建立平面直角坐标系；
（2）建筑物A的坐标为（3，1），请在图中标出A点的位置．
（3）建筑物B在大门北偏东45°的方向，并且B在花坛的正北方向处，请直接写出B点的坐标．
（4）在y轴上找一点C，使△ABC是以AB腰的等腰三角形，请直接写出点C的坐标．

在平面直角系中，已知A（-2，0），B（0，4），C（3，6）；

（1）当D（6，0）时，求四边形ABCD的面积；
（2）在x轴上找一点P，使△PBC的周长最小，并求出此时△PBC的周长．

如图，在边长均为1个单位长度的小正方形组成的网格中，点，点，点均为格点（每个小正方形的顶点叫做格点）．

（1）作点关于点的对称点；

（2）连接，将线段绕点顺时针旋转得点对应点，画出旋转后的线段；

（3）连接，求出四边形的面积．

如图，平行四边形ABCD（两组对边平行且相等）的边长AB=4，BC=2，若把它放在直角坐标系内，使AB在x轴上，点C在y轴上，点A的坐标是（-3，0），求点B、C、D的坐标．

在平面直角系中，已知A（﹣2，0），B（0，4），C（3，6）；

（1）当D（6，0）时，求四边形ABCD的面积；
（2）在x轴上找一点P，使△PBC的周长最小，并求出此时△PBC的周长．

如图，在平面直角坐标系xOy中，点A（0，8），点B（6，8）．

（1）只用直尺（没有刻度）和圆规，求作一个点P，使点P同时满足下列两个条件（要求保留作图痕迹，不必写出作法）：
①点P到A，B两点的距离相等；
②点P到∠xOy的两边的距离相等．
（2）在（1）作出点P后，写出点P的坐标．

如图，在平面直角坐标系中，A（﹣2，2），B（﹣3，﹣2）

（1）若点D与点A关于y轴对称，则点D的坐标为   ．
（2）将点B先向右平移5个单位再向上平移1个单位得到点C，则点C的坐标为   ．
（3）求A，B，C，D组成的四边形ABCD的面积。

在图的正方形网格中有一个三角形OAB，请你在网格中分别按下列要求画出图形
①画出△OAB向左平移3个单位后的三角形；
②画出△OAB绕点O旋转180°后的三角形；
③画出△OAB沿y轴翻折后的图形．

如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，的三个顶点、、均在格点上．

（1）将向左平移5个单位得到△，并写出点的坐标；

（2）画出△绕点顺时针旋转后得到的△，并写出点的坐标；

（3）在（2）的条件下，求△在旋转过程中扫过的面积（结果保留．

如图，在平面直角坐标系中，每个小正方形的边长为1，点A的坐标为（-3，2）
请按要求分别完成下列各小题：

（1）画出△ABC关于y轴对称的△，则点的坐标是       ；
（2）△ABC的面积是          ．

如图，在平面直角坐标系中，已知点A（2，3），B（6，3），连结AB，如果点P在直线y=x-1上 ，且点P到直线AB的距离小于1，那么称点P是线段AB的“邻近点”．

（1）判断点C（，）是否是线段AB的“邻近点”        ；
（2）若点Q（m，n）是线段AB的“邻近点”，则m的取值范围        ．

已知平面直角坐标系中有一点M（m-1，2m+3）
（1）当m为何值时，点M到x轴的距离为1？
（2）当m为何值时，点M到y轴的距离为2？

如图，在平面直角坐标系中，直线y=0．5x+2与x轴、y轴分别交于A、B两点，以AB为边在第二象限内作正方形ABCD，过点D作DE⊥x轴，垂足为E．

（1）求点A、B的坐标，并求边AB的长；
（2）求点D的坐标；
（3）你能否在x轴上找一点M，使△MDB的周长最小？如果能，请求出M点的坐标；如果不能，说明理由．