初中数学坐标与图形变化-旋转解答题

如图，△ABC三个顶点的坐标分别为A（﹣1，3），B（﹣4，1），C（﹣2，1）．

（1）请画出△ABC向右平移5个单位长度后得到的△A₁B₁C₁．

（2）请画出△A₁B₁C₁关于原点对称的△A₂B₂C₂．

（3）求四边形ABA₂B₂的面积．

阅读一段文字，再回答下列问题：已知在平面内两点的坐标为P₁（x₁，y₁），P₂（x₂，y₂），则该两点间距离公式为．同时，当两点在同一坐标轴上或所在直线平行于x轴、垂直于x轴时，两点间的距离公式可化简成|x2－x1|或|y2－y1|．
（1）若已知两点A（3，3），B（－2，－1），试求A，B两点间的距离；
（2）已知点M，N在平行于y轴的直线上，点M的纵坐标为7，点N的纵坐标为－2，试求M，N两点间的距离；
（3）已知一个三角形各顶点的坐标为A（0，5），B（－3，2），C（3，2），你能判定此三角形的形状吗？试说明理由．

在同一直角坐标系中分别描出点A（-3，0）、B（2，0）、C（1，3），再用线段将这三点首尾顺次连接起来，求△ABC的面积与周长．

如图，已知长方形ABCD的长为6，宽为4，请建立适当的平面直角坐标系，分别表示其各个顶点的坐标．

如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．

（1）求点C，D的坐标；
（2）若在y轴上存在点 M，连接MA，MB，使S_△MAB=S_{平行四边形ABDC}，求出点M的坐标．
（3）若点P在直线BD上运动，连接PC，PO．
①若P在线段BD之间时（不与B，D重合），求S_△CDP+S_△BOP的取值范围；
②若P在直线BD上运动，请直接写出∠CPO、∠DCP、∠BOP的数量关系．

如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ ABC的三个顶点的坐标分别为 A（﹣1，3）， B（﹣4，0）， C（0，0）

（1）画出将△ ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△ A ₁ B ₁ C ₁；

（2）画出将△ ABC绕原点 O顺时针方向旋转90°得到△ A ₂ B ₂ O；

（3）在 x轴上存在一点 P，满足点 P到 A ₁与点 A ₂距离之和最小，请直接写出 P点的坐标．

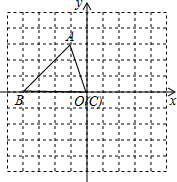
如图，在平面直角坐标系中，四边形OABC是边长为2的正方形，顶点A、C分别在x，y轴的正半轴上．点Q在对角线OB上，且QO=OC，连接CQ并延长CQ交边AB于点P．则点P的坐标为             ．

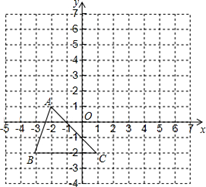
已知：如图，把△ABC向上平移3个单位长度，再向右平移2个单位长度，得到△ABC．

（1）在图中画出△ABC；
（2）写出点A、B、C的坐标；
（3）在轴上是否存在一点P，使得△PBC与△ABC面积相等？若存在，写出点P的坐标；若不存在，说明理由．

已知A（﹣1，2），B（﹣2，﹣1），将线段AB向右平移4个单位长度，再向下平移1个单位长度，得到线段A′B′．
（1）在给定的平面直角坐标系中描出A、B、A′、B′四个点，写出点A′、B′的坐标，并指出A、B、A′、B′四个点所在的象限；
（2）连接AA′与BB′，试判断线段AA′与BB′有怎样的位置关系和数量关系？

如图，在平面直角坐标系中，AD=8，OD=OB，▱ABCD的面积为24，求平行四边形的4个顶点的坐标．

如图，写出A、B、C关于x轴对称的点坐标，并作出与△ABC关于y轴对称的图形．

在边长为1的小正方形网格中，△AOB的顶点均在格点上．
（1）B点关于y轴的对称点坐标为           ；
（2）将△AOB向左平移3个单位长度得到△A₁O₁B₁，请画出△A₁O₁B₁；
（3）在（2）的条件下，A₁的坐标为         ．

在平面直角坐标系中，四边形是矩形，点，点，点．以点为中心，顺时针旋转矩形，得到矩形，点，，的对应点分别为，，．

（Ⅰ）如图①，当点落在边上时，求点的坐标；

（Ⅱ）如图②，当点落在线段上时，与交于点．

①求证；

②求点的坐标．

（Ⅲ）记为矩形对角线的交点，为的面积，求的取值范围（直接写出结果即可）．

如图，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．

（1）在图中作出△ABC关于y轴的对称图形△A₁B₁C₁；
（2）在y轴上找出一点P，使的PA+PB的值最小，直接画出点P的位置．

如图线段AB的端点在边长为1的正方形网格的格点上，现将线段AB绕点A按逆时针方向旋转90°得到线段AC．

（1）请你用尺规在所给的网格中画出线段AC及点B经过的路径；
（2）若将此网格放在一平面直角坐标系中，已知点A的坐标为（1，3），点B的坐标为（-2，-1），则点C的坐标为               ；
（3）线段AB在旋转到线段AC的过程中，线段AB扫过的区域的面积为           ；
（4）若有一张与（3）中所说的区域形状相同的纸片，将它围成一个几何体的侧面，则该几何体底面圆的半径长为