如图坐标平面上有一正五边形ABCDE,C、D两点坐标分别为(1,0)、(2,0).若在没有滑动的情况下,将此正五边形沿着x轴向右滚动,则滚动过程中,下列会经过点(75,0)的点是( )
A.点AB.点B C.点C D.点D
在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是
| A.(﹣2,1) | B.(﹣8,4) | C.(﹣8,4)或(8,﹣4) | D.(﹣2,1)或(2,﹣1) |
如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB饶点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是( )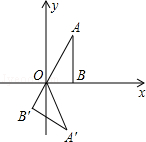
A.(2,﹣2 ) ) |
B.(2,﹣2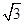 ) ) |
C.(2 ,﹣2) ,﹣2) |
D.(2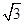 ,﹣2) ,﹣2) |
已知点A(3-p,2+p)先向x轴负方向平移2个单位,再 向y轴负方向平移3个单位得点B(p,-p),则点B的具体坐标为()
向y轴负方向平移3个单位得点B(p,-p),则点B的具体坐标为()
A. |
B. |
C. |
D. |
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是()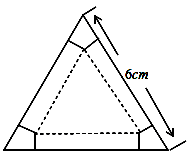
A.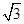 cm2 cm2 |
B. cm2 cm2 |
C.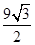 cm2 cm2 |
D.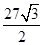 cm2 cm2 |
如图,在矩形 中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标为()
中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标为()
A.( ,
, )、(
)、( ,
, )B.(
)B.( ,
, )、(
)、( ,
, )
)
C.( ,
, )、(
)、( ,
, )D.(
)D.( ,
, ) 、(
) 、( ,
, )
)
将点B(5,-1)向上平移2个单位得到点A(a+b, a-b)。则()
| A.a=2, b=3 | B.a=3, b=2 | C.a=-3, b=-2 | D.a=-2, b=-3 |
如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A8的坐标是()
| A.(﹣8,0) | B.(0,8) | C.(0,8 ) ) |
D.(0,16) |
如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,保持上述运动过程,经过(2014,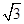 )的正六边形的顶点是()
)的正六边形的顶点是()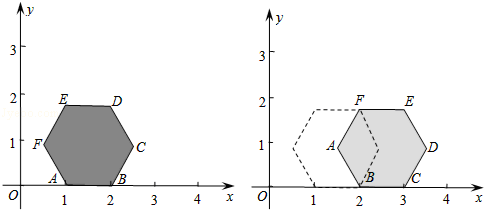
| A.C或E | B.B或D | C.A或E | D.B或F |
将点P(m+2,2m+4)向右平移1个单位得到P′,且P′在Y轴上, 那么P′坐标是()
那么P′坐标是()
| A.(-2,0) | B.(0,-2) | C.(1,0) | D. (0,1) (0,1) |
点P位于x轴下方,距离x轴5个单位 ,位于y轴右方,距离y轴3个单位,那么P点的坐标是()
,位于y轴右方,距离y轴3个单位,那么P点的坐标是()
| A.(5,-3) | B.(3,-5) | C.(-5,3) | D.(-3,5) |
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P坐标为()
A、(- ,
, ) B、(-
) B、(- ,2) C、(-1,
,2) C、(-1, ) D、(-1,2)
) D、(-1,2)
在平面直角坐标系中,已知A(1,1),要在坐标轴上找一点P,使得△PAO为等腰三角形,这样的P点有几个()
| A.9 | B.8 | C.7 | D.6 |