如图,在 中, , 是中线, ,一个以点 为顶点的 角绕点 旋转,使角的两边分别与 、 的延长线相交,交点分别为点 , , 与 交于点 , 与 交于点 .

(1)如图1,若 ,求证: ;
(2)如图2,在 绕点 旋转的过程中:
①探究三条线段 , , 之间的数量关系,并说明理由;
②若 , ,求 的长.
如图,边长为4的正六边形 的中心与坐标原点 重合, 轴,将正六边形 绕原点 顺时针旋转 次,每次旋转 .当 时,顶点 的坐标为 .

如图,在矩形 中, , 为 边的中点,将 绕点 顺时针旋转 ,点 的对应点为 ,点 的对应点为 ,过点 作 交 于点 ,连接 、 交于点 ,现有下列结论:
① ;
② ;
③ ;
④点 为 的外心.
其中正确的个数为

A.1个B.2个C.3个D.4个
已知 为直线 上一点, ,在等腰 中, , 交 于 , 为 的中点, 交 于 .
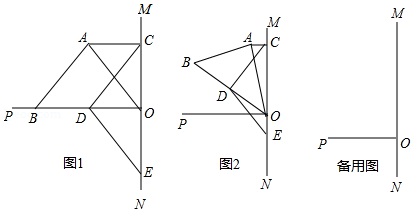
(1)如图1,若点 在 上,则
① (填“ ”,“ ”或“ ” ;
②线段 、 、 满足的等量关系式是 ;
(2)将图1中的等腰 绕 点顺时针旋转 ,如图2,那么(1)中的结论②是否成立?请说明理由;
(3)将图1中的等腰 绕 点顺时针旋转 ,请你在图3中画出图形,并直接写出线段 、 、 满足的等量关系式 .
如图,正方形 中, 是对角线 上的一个动点(不与 、 重合),连结 ,将 绕点 顺时针旋转 到 ,连结 交 于点 , 延长线与边 交于点 .
(1)连结 ,求证: ;
(2)若 ,求 的值;
(3)求证: .

已知:如图,在 中, , , .将 绕顶点 ,按顺时针方向旋转到△ 处,此时线段 与 的交点 恰好为 的中点,则线段 .

如图,在四边形 中, , , , , ,将 绕点 顺时针方向旋转后得△ ,当 恰好经过点 时,△ 为等腰三角形,则
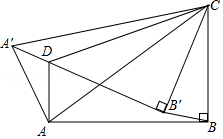
A. B. C. D.
如图,在 中, , .将 绕点 按顺时针方向旋转至
△ 的位置,点 恰好落在边 的中点处,则 的长为 .

将边长为1的正方形 绕点 按顺时针方向旋转到 的位置(如图),使得点 落在对角线 上, 与 相交于点 ,则 .(结果保留根号)

在 中,已知 , , .如图所示,将 绕点 按逆时针方向旋转 后得到△ .则图中阴影部分面积为

A. B. C. D.
如图, 中, ,将 绕点 顺时针旋转得到 ,点 落在线段 上,连接 .
(1)求证: 平分 ;
(2)试判断 与 的位置关系,并说明理由;
(3)若 ,求 的值.

如图,在矩形 中, , ,将矩形 绕点 逆时针旋转得到矩形 , 交 于点 ,且 ,则 的长为
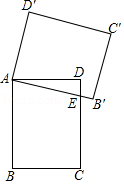
A.3B. C. D.