如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到△ ,使点 落在 上,边 交线段 于点 .若 ,则
度.
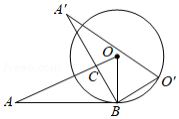
如图.将菱形 绕点 逆时针旋转 得到菱形 , .当 平分 时, 与 满足的数量关系是
| A. |
|
B. |
|
C. |
|
D. |
|
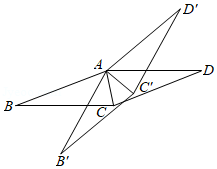
如图,在 中, ,将 绕点 逆时针旋转得到 ,点 , 的对应点分别为 , ,连接 .当点 , , 在同一条直线上时,下列结论一定正确的是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,将 绕点 顺时针旋转 得到△ ,已知 , ,则线段 扫过的图形(阴影部分)的面积为 .

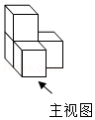
如图是由4个相同的小正方体堆成的物体,将它在水平面内顺时针旋转 后,其主视图是
| A. |
|
B. |
|
C. |
|
D. |
|
定义:平面上一点到图形最短距离为 ,如图, ,正方形 边长为2, 为正方形中心,当正方形 绕 旋转时,则 的取值范围为 .
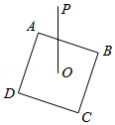
如图,在矩形 中,对角线 与 相交于点 , ,对角线 所在的直线绕点 顺时针旋转角 ,所得的直线 分别交 , 于点 , .
(1)求证: ;
(2)当旋转角 为多少度时,四边形 为菱形?试说明理由.

如图,点 为正方形 外一点, ,将 绕 点逆时针方向旋转 得到 , 的延长线交 于 点.
(1)试判定四边形 的形状,并说明理由;
(2)已知 , ,求 的长.

如图, 的顶点 , ,点 在 轴的正半轴上,延长 交 轴于点 .将 绕点 顺时针旋转得到△ ,当点 的对应点 落在 上时, 的延长线恰好经过点 ,则点 的坐标为

| A. |
, |
B. |
, |
C. |
, |
D. |
, |
如图所示,点 , , 对应的刻度分别为1,3,5,将线段 绕点 按顺时针方向旋转,当点 首次落在矩形 的边 上时,记为点 ,则此时线段 扫过的图形的面积为

| A. |
|
B. |
6 |
C. |
|
D. |
|
如图1,在 中, , ,点 , 分别在边 , 上,且 ,连接 .现将 绕点 顺时针方向旋转,旋转角为 ,如图2,连接 , , .
(1)当 时,求证: ;
(2)如图3,当 时,延长 交 于点 ,求证: 垂直平分 ;
(3)在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.

如图,在 中, , ,将 绕点 旋转得到 △ ,使点 的对应点 落在 上,在 上取点 ,使 ,那么点 到 的距离等于
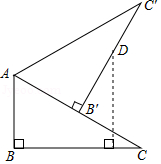
A. B. C. D.