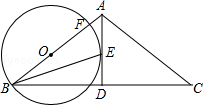
如图,在△ABC中,AB=AC,AD是角平分线,BE平分∠ABC交AD于点E,点O在AB上,以OB为半径的⊙O经过点E,交AB于点F
(1)求证:AD是⊙O的切线;
(2)若AC=4,∠C=30°,求 的长.
如图,将 绕点 顺时针旋转 得到 ,点 的对应点 恰好落在 的延长线上,连接 .
(1)求证: ;
(2)若 , ,求 , 两点旋转所经过的路径长之和.

如图,点是
的内心,
的延长线和
的外接圆
相交于点
,过
作直线
.
(1)求证:是
的切线;
(2)若,
,求优弧
的长.

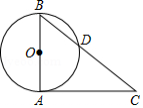
如图,已知⊙O是△ABC的外接圆,且BC为⊙O的直径,在劣弧上取一点D,使
,将△ADC沿AD对折,得到△ADE,连接CE.
(1)求证:CE是⊙O的切线;
(2)若CECD,劣弧
的弧长为π,求⊙O的半径.

如图,已知是
的直径,
与
相切于点
,且
.
(1)求证:是
的切线;
(2)延长交
于点
.若
,
的半径为2,求
的长.(结果保留

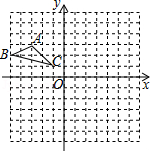
在边长为1的正方形网格中如图所示.
①以点为位似中心,作出
的位似图形△
,使其位似比为
.且△
位于点
的异侧,并表示出
的坐标.
②作出绕点
顺时针旋转
后的图形△
.
③在②的条件下求出点经过的路径长.
如图,为半圆
的直径,点
为半圆上任一点.
(1)若,过点
作半圆
的切线交直线
于点
.求证:
;
(2)若,过点
作
的平行线交半圆
于点
.当以点
,
,
,
为顶点的四边形为菱形时,求
的长.

如图,四边形是正方形,以边
为直径作
,点
在
边上,连结
交
于点
,连结
并延长交
于点
.
(1)求证:;
(2)若,
,求劣弧
的长.(结果保留

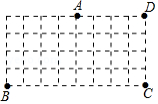
如图是由边长为1的小正方形组成的网格,每个小正方形的顶点叫做格点,点
,
,
,
均在格点上,在网格中将点
按下列步骤移动:
第一步:点绕点
顺时针旋转
得到点
;
第二步:点绕点
顺时针旋转
得到点
;
第三步:点绕点
顺时针旋转
回到点
.
(1)请用圆规画出点经过的路径;
(2)所画图形是 对称图形;
(3)求所画图形的周长(结果保留.
如图,是
的直径,
切
于点
,
交
于点
.已知
的半径为6,
.
(1)求的度数.
(2)求的长.(结果保留
如图1和2,中,
,
,
.点
为
延长线上一点,过点
作
切
于点
,设
.
(1)如图1,为何值时,圆心
落在
上?若此时
交
于点
,直接指出
与
的位置关系;
(2)当时,如图2,
与
交于点
,求
的度数,并通过计算比较弦
与劣弧
长度的大小;
(3)当与线段
只有一个公共点时,直接写出
的取值范围.

如图,点在数轴上对应的数为26,以原点
为圆心,
为半径作优弧
,使点
在
右下方,且
,在优弧
上任取一点
,且能过
作直线
交数轴于点
,设
在数轴上对应的数为
,连接
.
(1)若优弧上一段
的长为
,求
的度数及
的值;
(2)求的最小值,并指出此时直线
与
所在圆的位置关系;
(3)若线段的长为12.5,直接写出这时
的值.

如图,,
为
中点,点
在线段
上(不与点
,
重合),将
绕点
逆时针旋转
后得到扇形
,
,
分别切优弧
于点
,
,且点
,
在
异侧,连接
.
(1)求证:;
(2)当时,求
的长(结果保留
;
(3)若的外心在扇形
的内部,求
的取值范围.

在中,
,
分别是
两边的中点,如果
上的所有点都在
的内部或边上,则称
为
的中内弧.例如,图1中
是
的一条中内弧.

(1)如图2,在中,
,
,
分别是
,
的中点,画出
的最长的中内弧
,并直接写出此时
的长;
(2)在平面直角坐标系中,已知点,
,
,
,在
中,
,
分别是
,
的中点.
①若,求
的中内弧
所在圆的圆心
的纵坐标的取值范围;
②若在中存在一条中内弧
,使得
所在圆的圆心
在
的内部或边上,直接写出
的取值范围.