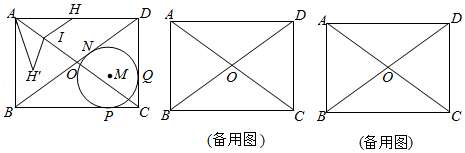
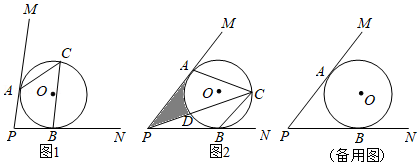
如图,在矩形 中,对角线相交于点 , 为 的内切圆,切点分别为 , , , , .
(1)求 , ;
(2)点 从点 出发,沿线段 向点 以每秒3个单位长度的速度运动,当点 运动到点 时停止,过点 作 交 于点 ,设运动时间为 秒.
①将 沿 翻折得△ ,是否存在时刻 ,使点 恰好落在边 上?若存在,求 的值;若不存在,请说明理由;
②若点 为线段 上的动点,当 为正三角形时,求 的值.
结果如此巧合
下面是小颖对一道题目的解答.
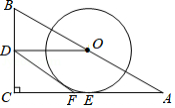
题目:如图, 的内切圆与斜边 相切于点 , , ,求 的面积.
解:设 的内切圆分别与 、 相切于点 、 , 的长为 .
根据切线长定理,得 , , .
根据勾股定理,得 .
整理,得 .
所以
.
小颖发现12恰好就是 ,即 的面积等于 与 的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
已知: 的内切圆与 相切于点 , , .
可以一般化吗?
(1)若 ,求证: 的面积等于 .
倒过来思考呢?
(2)若 ,求证 .
改变一下条件
(3)若 ,用 、 表示 的面积.
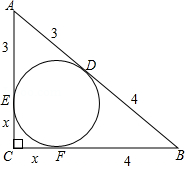
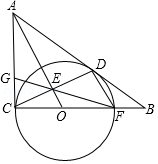
如图, 、 是 的切线, 、 是切点, 是 的直径,连接 ,交 于点 ,交 于点 .
(1)求证: ;
(2)若 恰好是 的中点,且四边形 的面积是 ,求阴影部分的面积;
(3)若 ,且 ,求切线 的长.

如图,顶点为的抛物线
与
轴交于
,
两点,与
轴交于点
.
(1)求这条抛物线对应的函数表达式;
(2)问在轴上是否存在一点
,使得
为直角三角形?若存在,求出点
的坐标;若不存在,说明理由.
(3)若在第一象限的抛物线下方有一动点,满足
,过
作
轴于点
,设
的内心为
,试求
的最小值.
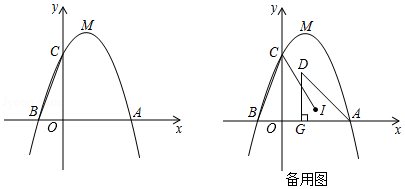
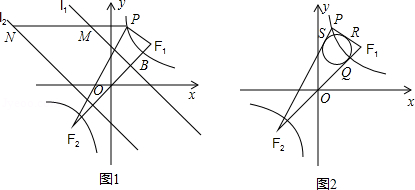
如图1所示,已知:点A(﹣2,﹣1)在双曲线 上,直线l1:y=﹣x+2,直线l2与l1关于原点成中心对称,F1(2,2),F2(﹣2,﹣2)两点间的连线与曲线C在第一象限内的交点为B,P是曲线C上第一象限内异于B的一动点,过P作x轴平行线分别交l1,l2于M,N两点.
(1)求双曲线C及直线l2的解析式;
(2)求证: ;
(3)如图2所示,△PF1F2的内切圆与F1F2,PF1,PF2三边分别相切于点Q,R,S,求证:点Q与点B重合.(参考公式:在平面坐标系中,若有点A(x1,y1),B(x2,y2),则A、B两点间的距离公式为 .
如图, 的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为 为 的整数),过点 作 的切线交 延长线于点 .
(1)通过计算比较直径和劣弧 长度哪个更长;
(2)连接 ,则 和 有什么特殊位置关系?请简要说明理由;
(3)求切线长 的值.

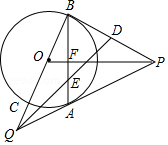
如图, 是 外的一点, 、 是 的两条切线, 、 是切点, 交 于点 ,延长 交 于点 ,交 的延长交于点 ,连接 .
(1)求证: ;
(2)设 为 的中点, 交 于点 ,若 的半径为3, ,求 的值.
已知 的两边分别与 相切于点 , , 的半径为 .
(1)如图1,点 在点 , 之间的优弧上, ,求 的度数;
(2)如图2,点 在圆上运动,当 最大时,要使四边形 为菱形, 的度数应为多少?请说明理由;
(3)若 交 于点 ,求第(2)问中对应的阴影部分的周长(用含 的式子表示).
如图, 与 的直角边 和斜边 分别相切于点 、 ,与边 相交于点 , 与 相交于点 ,连接 并延长交 边于点 .
(1)求证: ;
(2)若 , ,求 的长.
如图, 为 的内接三角形, 为 的直径,过点 作 的切线交 的延长线于点 .
(1)求证: ;
(2)过点 作 的切线 交 于点 ,求证: ;
(3)若点 为直径 下方半圆的中点,连接 交 于点 ,且 , ,求 的长.
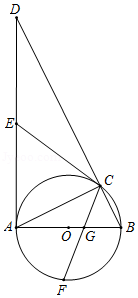
如图,在 中, , 是 边上的一点,以 为半径的 与边 相切于点 .
(1)若 , ,求 的半径;
(2)过点 作弦 于 ,连接 ,若 ,求证:四边形 是菱形.
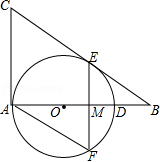
如图,在 中, 为 上一点,以点 为圆心, 为半径做圆,与 相切于点 ,过点 作 交 的延长线于点 ,且 .
(1)求证: 为 的切线;
(2)若 , ,求 的长.
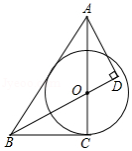
如图,在平行四边形 中, ,垂足为点 ,以 为直径的 与边 相切于点 ,连接 交 于点 ,连接 .
(1)求证: .
(2)若 ,求 的值.
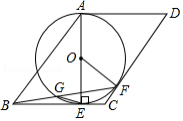
如图,在 中, ,点 , 分别为 , 的中点,连接 ,作 与 相切于点 ,在 边上取一点 ,使 ,连接 .
(1)判断直线 与 的位置关系,并说明理由;
(2)当 , 时,求 的半径.