如图,已知 是等边三角形 的外接圆,点 在圆上,在 的延长线上有一点 ,使 , 交 于 .
(1)求证: 是 的切线;
(2)求证: .

在等腰 中, ,以 为直径的 分别与 , 相交于点 , ,过点 作 ,垂足为点 .
(1)求证: 是 的切线;
(2)分别延长 , ,相交于点 , , 的半径为6,求阴影部分的面积.

如图,已知 是 的直径,过 点作 ,交弦 于点 ,交 于点 ,且使 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

如图,已知 是 的直径,点 为 延长线上的一点,点 为圆上一点,且 , .
(1)求证: ;
(2)求证: 是 的切线.

如图, 是 的外接圆, 为直径,弦 , 交 的延长线于点 .
(1)求证: ;
(2)求证: 是 的切线.

如图,已知在 中, ,以 为直径的 与 交于点 ,点 是 的中点,连接 , .
(1)若 ,求 ;
(2)求证: 是 的切线.
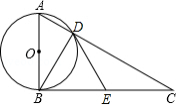
如图,已知 是 的直径,点 为圆上一点,点 为 延长线上一点, , .
(1)求证: 是 的切线.
(2)若 的直径为8,求阴影部分的面积.
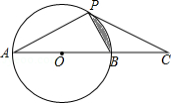
如图,点 是 直径 延长线上的一点, 在 上, ,
(1)求证: 是 的切线;
(2)若 的半径为2,求 的面积.

如图, 是 的直径,点 是 上一点,且 , 与 交于点 .
(1)求证: 是 的切线;
(2)若 平分 ,求证: ;
(3)在(2)的条件下,延长 、 交于点 ,若 , ,求 的长.
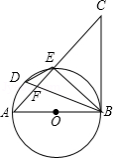
如图,在 中, 为直径, 、 为圆上两点, 为圆外一点,且 .
(1)求证: 为 的切线.
(2)若 , ,求 的半径.

如图,在 中, 为 上一点,且 ,以 为直径作 ,交 于点 ,连接 ,过 作 于点 , .
(1)求证: 是 的切线;
(2)若 , ,求 的直径 的长.

如图,已知 为 的角平分线, , ,以 为圆心, 为半径的圆分别交 , 于点 , ,连接 并延长交 于点 .
(1)求证: 是 的切线;
(2)求 的值;
(3)求 的值.

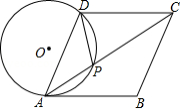
如图,在菱形 中,点 在对角线 上,且 , 是 的外接圆.
(1)求证: 是 的切线;
(2)若 , ,求 的半径.
如图, 是 的直径,弦 ,垂足为 ,连接 ,过 上一点 作 交 的延长线于点 ,连接 交 于点 ,且 ,连接 .
(1)求证: ;
(2)求证: 是 的切线;
(3)延长 交 的延长线于点 ,若 , ,求 的值.
