通过对下面数学模型的研究学习，解决问题．
【模型呈现】
如图，在 ， ，将斜边 绕点 顺时针旋转 得到 ，过点 作 于点 ，可以推理得到 ，进而得到 ， ．
我们把这个数学模型称为“ 型”．
推理过程如下：
【模型应用】
如图，在 内接于 ， ， ，将斜边 绕点 顺时针旋转一定的角度得到 ，过点 作 于点 ， ， ，连接 交 于点 ．
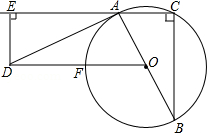
（1）求证： 是 的切线；
（2）连接 交 于点 ，连接 ．求证： ．
（·辽宁抚顺）电视节目“奔跑吧兄弟”播出后深受中小学生的喜爱，小刚想知道大家最喜欢哪位“兄弟”，于是在本校随机抽取了一部分学生进行抽查（每人只能选一个自己最喜欢的“兄弟”），将调查结果进行了整理后绘制成如图两幅不完整的统计图，请结合图中提供的信息解答下列问题：
（1）本次被调查的学生有 人．
（2）将两幅统计图补充完整．
（3）若小刚所在学校有2000名学生，请根据图中信息，估计全校喜欢“Angelababy”的人数．
（4）若从3名喜欢“李晨”的学生和2名喜欢“Angelababy”的学生中随机抽取两人参加文体活动，则两人都是喜欢“李晨”的学生的概率是 ．
（·辽宁朝阳）在学习概率的课堂上，老师提出问题：只有一张电影票，小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影，请你设计一个对小明和小刚都公平的方案．
甲同学的方案：将红桃2、3、4、5四张牌背面向上，小明先抽一张，小刚从剩下的三张牌中抽一张，若两张牌上的数字之和是奇数，则小明看电影，否则小刚看电影．
（1）甲同学的方案公平吗？请用列表或画树状图的方法说明；
（2）乙同学将甲的方案修改为只用红桃2、3、4三张牌，抽取方式及规则不变，乙的方案公平吗？（只回答，不说明理由）
（·辽宁朝阳）某校申报“跳绳特色运动”学校一年后，抽样调查了部分学生的“1分钟跳绳”成绩，并制成了下面的频数分布直方图（每小组含最小值，不含最大值）和扇形图．
（1）补全频数分布直方图，扇形图中m= ；
（2）若把每组中各个数据用这组数据的中间值代替（如A组80≤x＜100的中间值是（
=90次），则这次调查的样本平均数是多少？
（3）如果“1分钟跳绳”成绩大于或等于120次为优秀，那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人？
（·吉林长春）甲、乙两台机器共同加工一批零件，在加工过程中两台机器均改变了一次工作效率，从工作开始到加工完这批零件两台机器恰好同时工作6小时，甲、乙两台机器各自加工的零件的个数
（个）与加工时间
（时）之间的函数图象分别为折线
与折线
，如图所示．
（1）求甲机器改变工作效率前每小时加工零件的个数；
（2）求乙机器改变工作效率后与之间的函数关系式；
（3）求这批零件的总个数．
（0＜k＜15）的图象交于点B，D，连接AD，BC，AD与x轴交于点E（﹣2，0）．
粤公网安备 44130202000953号