已知,如图①,若 是 中 的内角平分线,通过证明可得 ,同理,若 是 中 的外角平分线,通过探究也有类似的性质.请你根据上述信息,求解如下问题:
如图②,在 中, , , 是 的内角平分线,则 的 边上的中线长 的取值范围是 .
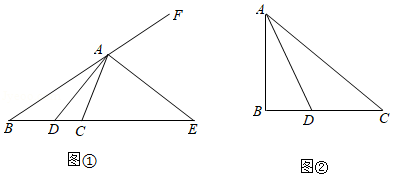
如图, 的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为 为 的整数),过点 作 的切线交 延长线于点 .
(1)通过计算比较直径和劣弧 长度哪个更长;
(2)连接 ,则 和 有什么特殊位置关系?请简要说明理由;
(3)求切线长 的值.

如图,已知 内接于 , 是 的直径, 的平分线交 于点 ,交 于点 ,连接 ,作 ,交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径和 的长.

如图,在 中, 为 的直径, 为 的弦,点 是 的中点,过点 作 的垂线,交 于点 ,交 于点 ,分别连接 , .
(1) 与 的数量关系是 ;
(2)求证: ;
(3)若 , ,求阴影部分图形的面积.

如图,四边形 中, , , , ,以 为圆心, 为半径作圆,延长 交 于点 ,延长 交 于点 ,连结 ,交 于点 .
(1)求证: 为 的切线;
(2)求 的值;
(3)求线段 的长.
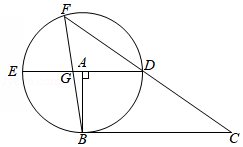
如图,在 中, , 是 上的一点,以 为直径的 与 相切于点 ,连接 , .
(1)求证: 平分 ;
(2)若 ,求 的值.

如图.在边长为6的正方形 中,点 , 分别在 , 上, 且 , ,垂足为 , 是对角线 的中点,连接 、则 的长为 .

如图,在四边形 中, , , ,点 、 分别在线段 、 上,且 , , .
(1)求证: ;
(2)求证:以 为直径的圆与 相切;
(3)若 , ,求 的面积.
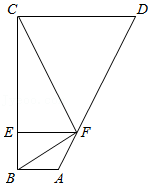
如图, 内接于 , 是 的直径 的延长线上一点, .过圆心 作 的平行线交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径及 的值.

如图, 是 的外接圆, 是 的直径, 于点 .
(1)求证: ;
(2)连接 并延长,交 于点 ,交 于点 ,连接 .若 的半径为5, ,求 和 的长.

定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)如图1, 是 中 的遥望角,若 ,请用含 的代数式表示 .
(2)如图2,四边形 内接于 , ,四边形 的外角平分线 交 于点 ,连结 并延长交 的延长线于点 .求证: 是 中 的遥望角.
(3)如图3,在(2)的条件下,连结 , ,若 是 的直径.
①求 的度数;
②若 , ,求 的面积.

如图,已知 , 为 的两条直径,连接 , , 于点 ,点 是半径 的中点,连接 .
(1)设 的半径为1,若 ,求线段 的长.
(2)连接 , ,设 与 交于点 ,
①求证: .
②若 ,求 的度数.

如图, 中, , 是 的外接圆, 的延长线交边 于点 .
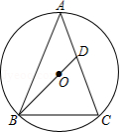
[小题1]求证: ;
[小题2]当 是等腰三角形时,求 的大小;
[小题3]当 , 时,求边 的长.
问题提出
(1)如图1,在 中, , , 的平分线交 于点 .过点 分别作 , .垂足分别为 , ,则图1中与线段 相等的线段是 .
问题探究
(2)如图2, 是半圆 的直径, . 是 上一点,且 ,连接 , . 的平分线交 于点 ,过点 分别作 , ,垂足分别为 , ,求线段 的长.
问题解决
(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知 的直径 ,点 在 上,且 . 为 上一点,连接 并延长,交 于点 .连接 , .过点 分别作 , ,垂足分别为 , .按设计要求,四边形 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设 的长为 ,阴影部分的面积为 .
①求 与 之间的函数关系式;
②按照“少儿活动中心”的设计要求,发现当 的长度为 时,整体布局比较合理.试求当 时.室内活动区(四边形 的面积.
