如图1,在 中, , ,点 是 边上一点(含端点 、 ,过点 作 垂直于射线 ,垂足为 ,点 在射线 上,且 ,连接 、 .

(1)求证: ;
(2)如图2,连接 ,点 、 、 分别为线段 、 、 的中点,连接 、 、 .求 的度数及 的值;
(3)在(2)的条件下,若 ,直接写出 面积的最大值.
如图,先将矩形纸片 沿 折叠 边与 在 的异侧), 交 于点 ;再将纸片折叠,使 与 在同一条直线上,折痕为 .若 ,纸片宽 ,则 .

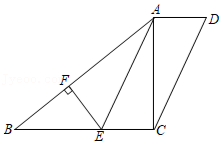
在等腰 中, , 是直角三角形, , ,连接 、 ,点 是 的中点,连接 .
(1)当 ,点 在边 上时,如图①所示,求证: ;
(2)当 ,把 绕点 逆时针旋转,顶点 落在边 上时,如图②所示,当 ,点 在边 上时,如图③所示,猜想图②、图③中线段 和 又有怎样的数量关系?请直接写出你的猜想,不需证明.

如图1, 中, , 为锐角.要在对角线 上找点 , ,使四边形 为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案

| A. |
甲、乙、丙都是 |
B. |
只有甲、乙才是 |
| C. |
只有甲、丙才是 |
D. |
只有乙、丙才是 |
如图,在四边形 中,对角线 与 交于点 ,已知 , ,过点 作 ,分别交 、 于点 , ,连接 , .
(1)求证:四边形 是菱形:
(2)设 , , ,求 的长.
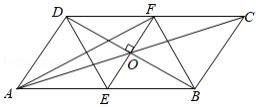
如图,在四边形 中, ,点 在 上, , ,垂足为 .
(1)求证:四边形 是平行四边形;
(2)若 平分 , , ,求 和 的长.
如图,在四边形 中, , , 分别平分 , ,并交线段 , 于点 , (点 , 不重合).在线段 上取点 , (点 在 之间),使 .当点 从点 匀速运动到点 时,点 恰好从点 匀速运动到点 .记 , ,已知 ,当 为 中点时, .
(1)判断 与 的位置关系,并说明理由.
(2)求 , 的长.
(3)若 .
①当 时,通过计算比较 与 的大小关系.
②连结 ,当 所在直线经过四边形 的一个顶点时,求所有满足条件的 的值.

如图,已知 , 为 的两条直径,连接 , , 于点 ,点 是半径 的中点,连接 .
(1)设 的半径为1,若 ,求线段 的长.
(2)连接 , ,设 与 交于点 ,
①求证: .
②若 ,求 的度数.

已知, 中, , 是 边上一点,作 ,分别交边 , 于点 , .
(1)若 (如图 ,求证: .
(2)若 ,过点 作 ,交 (或 的延长线)于点 .试猜想:线段 , 和 之间的数量关系,并就 情形(如图 说明理由.
(3)若点 与 重合(如图 , ,且 .
①求 的度数;
②设 , , ,试证明: .

如图,在平面直角坐标系中,四边形 的边 在 轴上,点 在 轴的负半轴上,直线 ,且 , ,将经过 、 两点的直线 向右平移,平移后的直线与 轴交于点 ,与直线 交于点 ,设 的长为 .
(1)四边形 的面积为 ;
(2)设四边形 被直线 扫过的面积(阴影部分)为 ,请直接写出 关于 的函数解析式;
(3)当 时,直线 上有一动点 ,作 直线 于点 ,交 轴于点 ,将 沿直线 折叠得到 ,探究:是否存在点 ,使点 恰好落在坐标轴上?若存在,请求出点 的坐标;若不存在,请说明理由.

如图,在平面直角坐标系中,四边形 的边 在 轴上,点 在 轴的负半轴上,直线 ,且 , ,将经过 、 两点的直线 向右平移,平移后的直线与 轴交于点 ,与直线 交于点 ,设 的长为 .
(1)四边形 的面积为 ;
(2)设四边形 被直线 扫过的面积(阴影部分)为 ,请直接写出 关于 的函数解析式;
(3)当 时,直线 上有一动点 ,作 直线 于点 ,交 轴于点 ,将 沿直线 折叠得到 ,探究:是否存在点 ,使点 恰好落在坐标轴上?若存在,请求出点 的坐标;若不存在,请说明理由.

如图,四边形 是平行四边形, , , 是 的中点, 是 延长线上一点.
(1)若 ,求证: ;
(2)在(1)的条件下,若 的延长线与 交于点 ,试判定四边形 是否为平行四边形?并证明你的结论(请先补全图形,再解答);
(3)若 , 与 垂直吗?若垂直给出证明,若不垂直说明理由.

如图1,在平面直角坐标系中, 是坐标原点,抛物线 与 轴正半轴交于点 ,与 轴交于点 ,连接 ,点 , 分别是 , 的中点, ,且 始终保持边 经过点 ,边 经过点 ,边 与 轴交于点 ,边 与 轴交于点 .
(1)填空: 的长是 , 的度数是 度;
(2)如图2,当 ,连接 .
①求证:四边形 是平行四边形;
②判断点 是否在该抛物线的对称轴上,并说明理由;
(3)如图3,当边 经过点 时,(此时点 与点 重合),过点 作 ,交 延长线上于点 ,延长 到点 ,使 ,过点 作 ,在 上取一点 ,使得 (点 , 在直线 的同侧),连接 ,请直接写出 的长.

如图,已知抛物线 与 轴交于 、 两点,与 轴交于点
(1)求点 , , 的坐标;
(2)点 是此抛物线上的点,点 是其对称轴上的点,求以 , , , 为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点 ,使得 是等腰三角形?若存在,请求出点 的坐标;若不存在,请说明理由.
