在等腰 中, , 是直角三角形, , ,连接 、 ,点 是 的中点,连接 .
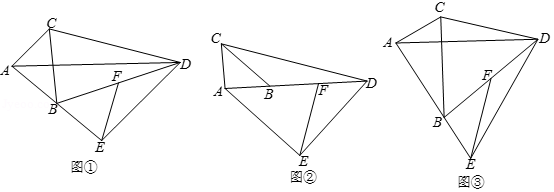
(1)当 ,点 在边 上时,如图①所示,求证: ;
(2)当 ,把 绕点 逆时针旋转,顶点 落在边 上时,如图②所示,当 ,点 在边 上时,如图③所示,猜想图②、图③中线段 和 又有怎样的数量关系?请直接写出你的猜想,不需证明.
推荐套卷
在等腰 中, , 是直角三角形, , ,连接 、 ,点 是 的中点,连接 .
(1)当 ,点 在边 上时,如图①所示,求证: ;
(2)当 ,把 绕点 逆时针旋转,顶点 落在边 上时,如图②所示,当 ,点 在边 上时,如图③所示,猜想图②、图③中线段 和 又有怎样的数量关系?请直接写出你的猜想,不需证明.
