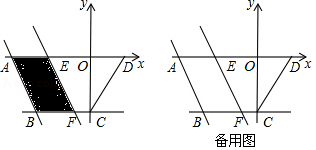
如图,在平面直角坐标系中,四边形 的边 在 轴上,点 在 轴的负半轴上,直线 ,且 , ,将经过 、 两点的直线 向右平移,平移后的直线与 轴交于点 ,与直线 交于点 ,设 的长为 .
(1)四边形 的面积为 ;
(2)设四边形 被直线 扫过的面积(阴影部分)为 ,请直接写出 关于 的函数解析式;
(3)当 时,直线 上有一动点 ,作 直线 于点 ,交 轴于点 ,将 沿直线 折叠得到 ,探究:是否存在点 ,使点 恰好落在坐标轴上?若存在,请求出点 的坐标;若不存在,请说明理由.
推荐套卷
如图,在平面直角坐标系中,四边形 的边 在 轴上,点 在 轴的负半轴上,直线 ,且 , ,将经过 、 两点的直线 向右平移,平移后的直线与 轴交于点 ,与直线 交于点 ,设 的长为 .
(1)四边形 的面积为 ;
(2)设四边形 被直线 扫过的面积(阴影部分)为 ,请直接写出 关于 的函数解析式;
(3)当 时,直线 上有一动点 ,作 直线 于点 ,交 轴于点 ,将 沿直线 折叠得到 ,探究:是否存在点 ,使点 恰好落在坐标轴上?若存在,请求出点 的坐标;若不存在,请说明理由.
