如图,等边三角形 的边长为4,点 是 的中心, ,绕点 旋转 ,分别交线段 、 于 、 两点,连接 ,给出下列四个结论:① ;② ;③四边形 的面积始终等于 ;④ 周长的最小值为6.上述结论中正确的个数是

A.1B.2C.3D.4
在边长为4的等边三角形 中, 为 边上的任意一点,过点 分别作 , ,垂足分别为 , ,则 .
【操作发现】
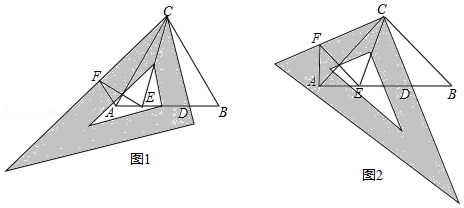
(1)如图1, 为等边三角形,先将三角板中的 角与 重合,再将三角板绕点 按顺时针方向旋转(旋转角大于 且小于 ,旋转后三角板的一直角边与 交于点 ,在三角板斜边上取一点 ,使 ,线段 上取点 ,使 ,连接 , .
①求 的度数;
② 与 相等吗?请说明理由;
【类比探究】
(2)如图2, 为等腰直角三角形, ,先将三角板的 角与 重合,再将三角板绕点 按顺时针方向旋转(旋转角大于 且小于 ,旋转后三角板的一直角边与 交于点 ,在三角板另一直角边上取一点 ,使 ,线段 上取点 ,使 ,连接 , .请直接写出探究结果:
① 的度数;
②线段 , , 之间的数量关系.
如图,在平面直角坐标系中,直线 与 轴交于点 ,以 为边长作等边三角形 ,过点 作 平行于 轴,交直线 于点 ,以 为边长作等边三角形 ,过点 作 平行于 轴,交直线 于点 ,以 为边长作等边三角形 , ,则点 的横坐标是 .

在 中, , ,将 绕点 按顺时针方向旋转,得到 ,旋转角为 ,点 的对应点为点 ,点 的对应点为点 ,连接 , .
(1)如图,当 时,延长 交 于点 .
①求证: 是等边三角形;
②求证: , ;
③请直接写出 的长;
(2)在旋转过程中,过点 作 垂直于直线 ,垂足为点 ,连接 ,当 ,且线段 与线段 无公共点时,请直接写出 的值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
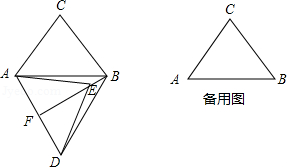
已知: 是等边三角形,点 在直线 上,连接 ,以 为边作等边三角形 ,将线段 绕点 顺时针旋转 ,得到线段 ,连接 、 、 .
(1)如图1,当点 在线段 上时,求证: ;
(2)如图1,当点 在线段 上时,求证:四边形 是平行四边形;
(3)如图2,当点 在线段 延长线上时,四边形 还是平行四边形吗?如果是,请证明你的结论;如果不是,请说明理由.

如图,在正方形 中,点 为对角线 上的一点,连接 , .
(1)如图1,求证: ;
(2)如图2,延长 交直线 于点 , 在直线 上,且 .
①求证: ;
②已知正方形 的边长为2,若点 在对角线 上移动,当 为等边三角形时,求线段 的长(直接写出结果,不必写出解答过程).

如图,△ ,△ ,△ , ,△ 为正整数)均为等边三角形,它们的边长依次为2,4,6, , ,顶点 , , , , 均在 轴上,点 是所有等边三角形的中心,则点 的坐标为 .

如图,点 在直线 上,过点 作 交直线 于点 ,以 为边在△ 外侧作等边三角形 ,再过点 作 ,分别交直线 和 于 , 两点,以 为边在△ 外侧作等边三角形 , 按此规律进行下去,则第 个等边三角形 的面积为 .(用含 的代数式表示)

如图,以边长为 的正三角形纸板的各顶点为端点,在各边上分别截取 长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中虚线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为 .

如图, 是等边三角形, ,分别以 , , 为圆心,以2为半径作弧,则图中阴影部分的面积是 .

已知: 和 均为等边三角形,连接 , ,点 , , 分别为 , , 中点.
(1)当 绕点 旋转时,如图1,则 的形状为 ,说明理由;
(2)在 旋转的过程中,当 , , 三点共线时,如图2,若 , ,求线段 的长;
(3)在 旋转的过程中,若 , ,则 的周长是否存在最大值和最小值,若存在,直接写出最大值和最小值;若不存在,说明理由.

如图,等边△ 的周长为1,作 于 ,在 的延长线上取点 ,使 ,连接 ,以 为边作等边△ ;作 于 ,在 的延长线上取点 ,使 ,连接 ,以 为边作等边△ ; 且点 , , , 都在直线 同侧,如此下去,则△ ,△ ,△ , ,△ 的周长和为 . ,且 为整数)
