已知： 和 均为等边三角形，连接 ， ，点 ， ， 分别为 ， ， 中点．
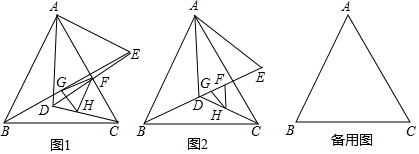
（1）当 绕点 旋转时，如图1，则 的形状为 ，说明理由；
（2）在 旋转的过程中，当 ， ， 三点共线时，如图2，若 ， ，求线段 的长；
（3）在 旋转的过程中，若 ， ，则 的周长是否存在最大值和最小值，若存在，直接写出最大值和最小值；若不存在，说明理由．
相关试题
某校八年级进行了一次数学测试，教务处抽取10%的学生成绩进行统计，结果如图7所示，（其中规定86分以上为优秀，76分～85分为良好；60～75为几个；59分以下为不及格）
（1）在抽取的学生中，不及格人数为
（2）小明按以下方法计算出所抽取学生数学测试成绩的平均分是：（90+80+65+45）÷4=70.根据所学的统计知识，判断小明的计算是否正确，若不正确，请写出正确的算式并计算出结果
（3）若抽取的学生中不及格学生的成绩恰好等于某一个优秀学生的分数，请估算出该校八年级优秀等级学生的人数
并把解集在数轴上表示出来
并在所给的数轴上表示出其解集．
（本小题满分14分）
在如图所示的一张矩形纸片
（
）中，将纸片折叠一次，使点
与
重合，再展开，折痕
交
边于
，交
边于
，分别连结
和
．
（1）求证：四边形
是菱形；（2）过
作
交
于
，求证：
（3）若
，
的面积为
，求的周长；
与y轴交于点A，E（0，b）为y轴上一动点，过点E的直线
与抛物线交于点B、C.
与
的面积。
时，
是以BC为斜边的直角三角形，若存在，求出b；若不存在，说明理由.相关知识点
推荐套卷
粤公网安备 44130202000953号