已知函数
,
均为一次函数,
为常数.

(1)如图1,将直线
绕点
逆时针旋转
得到直线
,直线
交
轴于点
.若直线
恰好是
,
中某个函数的图象,请直接写出点
坐标以及
可能的值;
(2)若存在实数
,使得
成立,求函数
,
图象间的距离;
(3)当
时,函数
图象分别交
轴,
轴于
,
两点,
图象交
轴于
点,将函数
的图象最低点
向上平移
个单位后刚好落在一次函数
图象上.设
的图象,线段
,线段
围成的图形面积为
,试利用初中知识,探究
的一个近似取值范围.(要求:说出一种得到
的更精确的近似值的探究办法,写出探究过程,得出探究结果,结果的取值范围两端的数值差不超过0.01.

 =9.
=9. )*2 =, (-1)*(2*3)= .
)*2 =, (-1)*(2*3)= . ,第二个数记为
,第二个数记为 ,第三个数记为
,第三个数记为 ……,第n个数记为
……,第n个数记为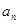 ,若
,若 ,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数。”
,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数。”
 ,
,





 粤公网安备 44130202000953号
粤公网安备 44130202000953号