在四边形 中, ,对角线 平分 .
(1)如图1,若 ,且 ,试探究边 、 与对角线 的数量关系并说明理由.
(2)如图2,若将(1)中的条件“ ”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若 ,探究边 、 与对角线 的数量关系并说明理由.

如图, 是反比例函数 在第一象限内的图象上一点,以 为顶点作等边 ,使 落在 轴上,则 的面积为

A. B. C. D.
如图, 是反比例函数 在第一象限内的图象上一点,以 为顶点作等边 ,使 落在 轴上,则 的面积为

A. B. C. D.
已知:如图,在平面直角坐标系 中,等边 的边长为6,点 在边 上,点 在边 上,且 ,反比例函数 的图象恰好经过点 和点 ,则 的值为

A. B. C. D.
如图, 和 都是等边三角形,点 、 、 三点在同一直线上,连接 , , 交 于点 .
(1)若 ,求证: ;
(2)若 , .
①求 的值;②求 的长.

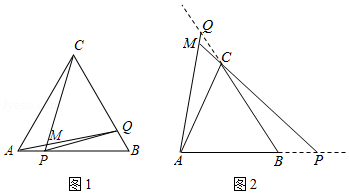
如图,点 、 分别是等边 边 、 上的动点(端点除外),点 、点 以相同的速度,同时从点 、点 出发.
(1)如图1,连接 、 .求证: ;
(2)如图1,当点 、 分别在 、 边上运动时, 、 相交于点 , 的大小是否变化?若变化,请说明理由;若不变,求出它的度数;
(3)如图2,当点 、 在 、 的延长线上运动时,直线 、 相交于 , 的大小是否变化?若变化,请说明理由;若不变,求出它的度数.
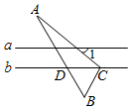
如图,直线 , 的顶点 在直线 上,边 与直线 相交于点 .若 是等边三角形, ,则 .
如图,已知等边 的边长是2,以 边上的高 为边作等边三角形,得到第一个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第二个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第三个等边△ ; .记△ 面积为 ,△ 面积为 ,△ 面积为 ,则 .

如图,等边 的边长为2, 的半径为1, 是 上的动点, 与 相切于 , 的最小值是

A.1B. C. D.2
如图,分别以等边三角形 的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若 ,则莱洛三角形的面积(即阴影部分面积)为

A. B. C. D.