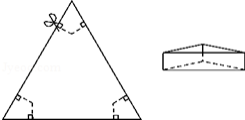
如图，以边长为 的正三角形纸板的各顶点为端点，在各边上分别截取 长的六条线段，过截得的六个端点作所在边的垂线，形成三个有两个直角的四边形．把它们沿图中虚线剪掉，用剩下的纸板折成一个底为正三角形的无盖柱形盒子，则它的容积为 ．
相关试题
= ．
（桂林）如图，以▱ABCO的顶点O为原点，边OC所在直线为x轴，建立平面直角坐标系，顶点A、C的坐标分别是（2，4）、（3，0），过点A的反比例函数
的图象交BC于D，连接AD，则四边形AOCD的面积是 ．
推荐套卷
如图，以边长为 的正三角形纸板的各顶点为端点，在各边上分别截取 长的六条线段，过截得的六个端点作所在边的垂线，形成三个有两个直角的四边形．把它们沿图中虚线剪掉，用剩下的纸板折成一个底为正三角形的无盖柱形盒子，则它的容积为 ．
（桂林）如图，以▱ABCO的顶点O为原点，边OC所在直线为x轴，建立平面直角坐标系，顶点A、C的坐标分别是（2，4）、（3，0），过点A的反比例函数的图象交BC于D，连接AD，则四边形AOCD的面积是 ．
粤公网安备 44130202000953号