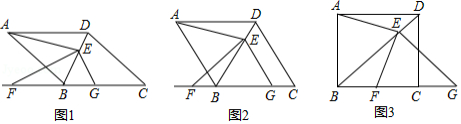
问题背景:如图1,在四边形 中, , , , , , 绕 点旋转,它的两边分别交 、 于 、 .探究图中线段 , , 之间的数量关系.
小李同学探究此问题的方法是:延长 到 ,使 ,连接 ,先证明 ,再证明 ,可得出结论,他的结论就是 ;
探究延伸1:如图2,在四边形 中, , , , , 绕 点旋转.它的两边分别交 、 于 、 ,上述结论是否仍然成立?请直接写出结论(直接写出"成立"或者"不成立" ,不要说明理由;
探究延伸2:如图3,在四边形 中, , , , 绕 点旋转.它的两边分别交 、 于 、 .上述结论是否仍然成立?并说明理由;
实际应用:如图4,在某次军事演习中,舰艇甲在指挥中心 处)北偏西 的 处.舰艇乙在指挥中心南偏东 的 处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以75海里 小时的速度前进,同时舰艇乙沿北偏东 的方向以100海里 小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达 、 处.且指挥中心观测两舰艇视线之间的夹角为 .试求此时两舰艇之间的距离.

阅读理解:
我们把满足某种条件的所有点所组成的图形,叫做符合这个条件的点的轨迹.
例如:角的平分线是到角的两边距离相等的点的轨迹.
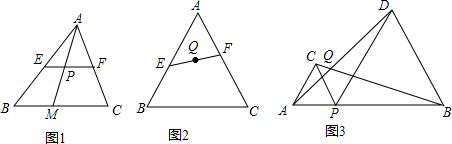
问题:如图1,已知 为 的中位线, 是边 上一动点,连接 交 于点 ,那么动点 为线段 中点.
理由: 线段 为 的中位线, ,
由平行线分线段成比例得:动点 为线段 中点.
由此你得到动点 的运动轨迹是: .
知识应用:
如图2,已知 为等边 边 、 上的动点,连接 ;若 ,且等边 的边长为8,求线段 中点 的运动轨迹的长.
拓展提高:
如图3, 为线段 上一动点(点 不与点 、 重合),在线段 的同侧分别作等边 和等边 ,连接 、 ,交点为 .
(1)求 的度数;
(2)若 ,求动点 运动轨迹的长.
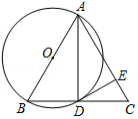
如图,在 中, ,以 为直径的 交 于点 ,过点 作 ,垂足为点 .
(1)求证: ;
(2)判断直线 与 的位置关系,并说明理由.
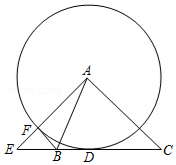
如图,在 中, ,以 为直径的 交 于点 ,交 于点 ,过点 作 ,与过点 的切线相交于点 ,连接 .
(1)求证: ;
(2)若 , ,求 的长.

如图,在 中, ,过 的中点 作 , ,垂足分别为点 、 .
(1)求证: ;
(2)若 ,求 的度数.

如图, , 平分 ,点 是射线 上一定点,点 在直线 上运动,连接 ,将 的两边射线 和 分别绕点 顺时针旋转 ,旋转后角的两边分别与射线 交于点 和点 .

(1)如图1,当点 在射线 上时,
①请判断线段 与 的数量关系,直接写出结论;
②请探究线段 , 和 之间的数量关系,写出结论并证明;
(2)如图2,当点 在射线 的反向延长线上时, 交射线 于点 ,若 , ,请直接写出线段 和 的长.
如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

如图,在 中, , 与 相切于点 ,过点 作 的垂线交 的延长线于点 ,交 于点 ,连结 .
(1)求证: 是 的切线.
(2)若 , ,求 的长.
如图, 为等腰直角三角形,延长 至点 使 , 是矩形,其对角线 , 交于点 ,连接 交 于点 .
(1)求证: ;
(2)求 的值.

已知:如图,四边形 为平行四边形,点 、 、 、 在同一直线上, .
求证:(1) ;
(2) .

如图,在 中,过 点作 于点 ,交 于点 ,过 点作 于点 ,交 于点 .
(1)求证:四边形 是平行四边形;
(2)已知 , ,求 的长.
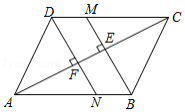
在菱形 中,点 为对角线 上一点,点 , 在直线 上,且 , .
(1)如图1,求证: ;
(2)如图2,当 时,求证: ;
(3)如图3,当 ,点 在线段 上时,线段 , , 的数量关系如何?(请直接写出你猜想的结论)