阅读理解:
我们把满足某种条件的所有点所组成的图形,叫做符合这个条件的点的轨迹.
例如:角的平分线是到角的两边距离相等的点的轨迹.
问题:如图1,已知 为 的中位线, 是边 上一动点,连接 交 于点 ,那么动点 为线段 中点.
理由: 线段 为 的中位线, ,
由平行线分线段成比例得:动点 为线段 中点.
由此你得到动点 的运动轨迹是: .
知识应用:
如图2,已知 为等边 边 、 上的动点,连接 ;若 ,且等边 的边长为8,求线段 中点 的运动轨迹的长.
拓展提高:
如图3, 为线段 上一动点(点 不与点 、 重合),在线段 的同侧分别作等边 和等边 ,连接 、 ,交点为 .
(1)求 的度数;
(2)若 ,求动点 运动轨迹的长.

相关知识点
推荐套卷


 的值;
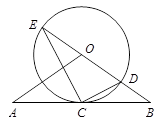
的值; BAE=
BAE=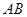 经过
经过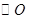 上的点
上的点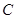 ,并且
,并且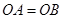 ,
,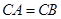 ,
,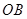 于
于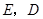 ,连接
,连接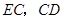 .
. [
[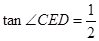 ,
,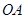 的长.
的长.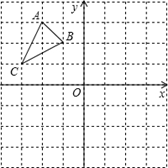


 粤公网安备 44130202000953号
粤公网安备 44130202000953号