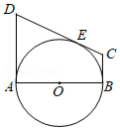
如图所示, 是 的直径, 和 分别切 于 , 两点, 与 有公共点 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
综合与实践
问题情境:
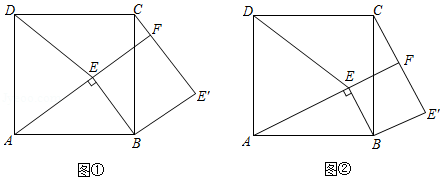
如图①,点 为正方形 内一点, ,将 绕点 按顺时针方向旋转 ,得到 (点 的对应点为点 .延长 交 于点 ,连接 .
猜想证明:
(1)试判断四边形 的形状,并说明理由;
(2)如图②,若 ,请猜想线段 与 的数量关系并加以证明;
解决问题:
(3)如图①,若 , ,请直接写出 的长.
阅读与思考
如图是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
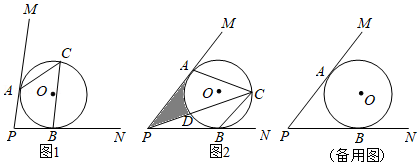
年 月 日星期日 没有直角尺也能作出直角 今天,我在书店一本书上看到下面材料:木工师傅有一块如图①所示的四边形木板,他已经在木板上画出一条裁割线 ,现根据木板的情况,要过 上的一点 ,作出 的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢? 办法一:如图①,可利用一把有刻度的直尺在 上量出 ,然后分别以 , 为圆心,以 与 为半径画圆弧,两弧相交于点 ,作直线 ,则 必为 .
办法二:如图②,可以取一根笔直的木棒,用铅笔在木棒上点出 , 两点,然后把木棒斜放在木板上,使点 与点 重合,用铅笔在木板上将点 对应的位置标记为点 ,保持点 不动,将木棒绕点 旋转,使点 落在 上,在木板上将点 对应的位置标记为点 .然后将 延长,在延长线上截取线段 ,得到点 ,作直线 ,则 . 我有如下思考:以上两种办法依据的是什么数学原理呢?我还有什么办法不用直角尺也能作出垂线呢? |
任务:
(1)填空:“办法一”依据的一个数学定理是 ;
(2)根据“办法二”的操作过程,证明 ;
(3)①尺规作图:请在图③的木板上,过点 作出 的垂线(在木板上保留作图痕迹,不写作法);
②说明你的作法所依据的数学定理或基本事实(写出一个即可).
如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高 .他俩在小明家的窗台 处,测得商业大厦顶部 的仰角 的度数,由于楼下植物的遮挡,不能在 处测得商业大厦底部 的俯角的度数.于是,他俩上楼来到小华家,在窗台 处测得大厦底部 的俯角 的度数,竟然发现 与 恰好相等.已知 , , 三点共线, , , , ,试求商业大厦的高 .

在 中, , 交 的延长线于点 .

特例感知:
(1)将一等腰直角三角尺按图1所示的位置摆放,该三角尺的直角顶点为 ,一条直角边与 重合,另一条直角边恰好经过点 .通过观察、测量 与 的长度,得到 .请给予证明.
猜想论证:
(2)当三角尺沿 方向移动到图2所示的位置时,一条直角边仍与 边重合,另一条直角边交 于点 ,过点 作 垂足为 .此时请你通过观察、测量 、 与 的长度,猜想并写出 、 与 之间存在的数量关系,并证明你的猜想.
联系拓展:
(3)当三角尺在图2的基础上沿 方向继续移动到图3所示的位置(点 在线段 上,且点 与点 不重合)时,请你判断(2)中的猜想是否仍然成立?(不用证明)
如图,在 中, .
(1)尺规作图:作 的外接圆 ;作 的角平分线交 于点 ,连接 .(不写作法,保留作图痕迹)
(2)若 , ,求 的长.

已知 的两边分别与 相切于点 , , 的半径为 .
(1)如图1,点 在点 , 之间的优弧上, ,求 的度数;
(2)如图2,点 在圆上运动,当 最大时,要使四边形 为菱形, 的度数应为多少?请说明理由;
(3)若 交 于点 ,求第(2)问中对应的阴影部分的周长(用含 的式子表示).
如图, 中, ,顶点 , 都在反比例函数 的图象上,直线 轴,垂足为 ,连结 , ,并延长 交 于点 ,当 时,点 恰为 的中点,若 , .
(1)求反比例函数的解析式;
(2)求 的度数.

如图, 中, ,点 , 在边 上, ,点 在 的延长线上, .
(1)求证: ;
(2)若 ,则 .

问题呈现
如图1,在边长为1的正方形网格中,连接格点 , 和 , , 和 相交于点 ,求 的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点 , ,可得 ,则 ,连接 ,那么 就变换到 中.
问题解决
(1)直接写出图1中 的值为 2 ;
(2)如图2,在边长为1的正方形网格中, 与 相交于点 ,求 的值;
思维拓展
(3)如图3, , ,点 在 上,且 ,延长 到 ,使 ,连接 交 的延长线于点 ,用上述方法构造网格求 的度数.

如图,在 中, , 于点 , 于点 ,以点 为圆心, 为半径作半圆,交 于点 .
(1)求证: 是 的切线;
(2)若点 是 的中点, ,求图中阴影部分的面积;
(3)在(2)的条件下,点 是 边上的动点,当 取最小值时,直接写出 的长.
