已知:如图,正方形中,
是边
上一点,
,
,垂足分别是点
、
.
(1)求证:;
(2)连接,如果
.求证:
.

已知任一平面封闭图形,现在其外部存在一水平放置的矩形,使得矩形每条边都与该图形有至少一个交点,且构成该图形的所有点都在矩形内部或矩形边上,那么就称这个矩形为“该图形的矩形”,且这个矩形的水平长成为该图形的宽,铅直高称为该图形的高.如图,边长为1的菱形的一条边水平放置,已知“该菱形的矩形”的“高”是“宽”的,则该“菱形的矩形”的“宽”为 .

如图,已知 ,点 、 在射线 上(点 在点 、 之间),半径长为2的 与直线 相切,半径长为3的 与 相交,那么 的取值范围是

| A. |
|
B. |
|
C. |
|
D. |
|
已知在平面直角坐标系中(如图),已知抛物线
经过点
,对称轴是直线
,顶点为
.
(1)求这条抛物线的表达式和点的坐标;
(2)点在对称轴上,且位于顶点上方,设它的纵坐标为
,联结
,用含
的代数式表示
的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点在
轴上.原抛物线上一点
平移后的对应点为点
,如果
,求点
的坐标.
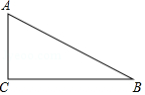
已知:如图,四边形中,
,
,
是对角线
上一点,且
.
(1)求证:四边形是菱形;
(2)如果,且
,求证:四边形
是正方形.

我们规定:一个正边形
为整数,
的最短对角线与最长对角线长度的比值叫做这个正
边形的“特征值”,记为
,那么
.
如图,已知,
,
,
.分别以点
、
为圆心画圆.如果点
在
内,点
在
外,且
与
内切,那么
的半径长
的取值范围是 .
如图,抛物线 经过点 ,与 轴的负半轴交于点 ,与 轴交于点 ,且 ,抛物线的顶点为点 .
(1)求这条抛物线的表达式;
(2)联结 、 、 、 ,求四边形 的面积;
(3)如果点 在 轴的正半轴上,且 ,求点 的坐标.

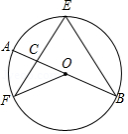
已知:如图, 是 的外接圆, ,点 在边 上, , .
(1)求证: ;
(2)如果点 在线段 上(不与点 重合),且 ,求证:四边形 是平行四边形.

如图,在 中, , ,点 在边 上,且 , ,垂足为点 ,联结 ,求:
(1)线段 的长;
(2) 的余切值.

如图, 是 的直径, , 是 的弦,且 , 与 交于点 ,连接 ,若 ,则 的度数是
| A. |
|
B. |
|
C. |
|
D. |
|