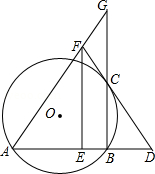
如图, 已知: 是 的弦, 过点 作 交 于点 ,过点 作 的切线交 的延长线于点 ,取 的中点 ,过点 作 交 的延长线于点 ,连接 并延长交 的延长线于点 .
求证:
(1) ;
(2) .
如图,在 中,连接 ,在 的延长线上取一点 ,在 的延长线上取一点 ,使 ,连接 、 .
求证: .

如图,在菱形中,
,
,点
是这个菱形内部或边上的一点,若以点
、
、
为顶点的三角形是等腰三角形,则
、
、
两点不重合)两点间的最短距离为 .

如图,在正方形 中,连接 ,点 是 的中点,若 、 是边 上的两点,连接 、 ,并分别延长交边 于两点 、 ,则图中的全等三角形共有

| A. |
2对 |
B. |
3对 |
C. |
4对 |
D. |
5对 |
如图, 在 中, , , . 若 是 的中位线, 延长 交 的外角 的平分线于点 ,则线段 的长为

| A. |
A . 7B . 8C . 9D . 10 |
如图所示,在平面直角坐标系中, 为坐标原点,且 是等腰直角三角形, ,点 .
(1)求点 的坐标;
(2)求经过 、 、 三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点 ,使四边形 的面积最大?若存在,求出点 的坐标;若不存在,请说明理由.
如图,在三边互不相等的 中, 、 、 分别是 、 、 边的中点,连接 ,过点 作 交 的延长线于点 ,连接 、 交于点 ,则图中全等三角形共有
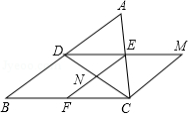
| A. |
3对 |
B. |
4对 |
C. |
5对 |
D. |
6对 |
如图,在 中, , , , 的高 与角平分线 交于点 ,则 的值为
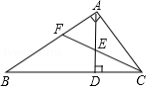
| A. |
|
B. |
|
C. |
|
D. |
|
在图1,2,3中,已知,
,点
为线段
上的动点,连接
,以
为边向上作菱形
,且
.
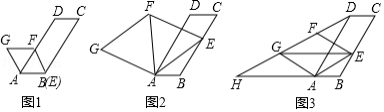
(1)如图1,当点与点
重合时,
;
(2)如图2,连接.
①填空:
(填“
”,“
“,“
”
;
②求证:点在
的平分线上;
(3)如图3,连接,
,并延长
交
的延长线于点
,当四边形
是平行四边形时,求
的值.
如图,在平面直角坐标系中,点,
的坐标分别为
,
,
,
,连接
,以
为边向上作等边三角形
.
(1)求点的坐标;
(2)求线段所在直线的解析式.

在中,
,点
在以
为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图1中作弦,使
;
(2)在图2中以为边作一个
的圆周角.

我国古代数学名著《孙子算经》有估算方法:“方五,邪(通“斜” 七.见方求邪,七之,五而一.”译文为:如果正方形的边长为五,则它的对角线长为七.已知正方形的边长,求对角线长,则先将边长乘以七再除以五.若正方形的边长为1,由勾股定理得对角线长为
,依据《孙子算经》的方法,则它的对角线的长是 .