如图,在 中, , , ,以 的中点 为圆心, 的长为半径作半圆交 于点 ,则图中阴影部分的面积为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , ,直线 ,顶点 在直线 上,直线 交 于点 ,交 与点 ,若 ,则 的度数是
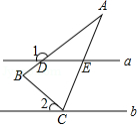
| A. |
|
B. |
|
C. |
|
D. |
|
综合与实践
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形中,
,
是
延长线上一点,且
,连接
,交
于点
,以
为一边在
的左下方作正方形
,连接
.试判断线段
与
的位置关系.
探究展示:勤奋小组发现,垂直平分
,并展示了如下的证明方法:
证明:,
.
,
.
四边形
是矩形,
.
.(依据
,
.
.
即是
的
边上的中线,
又,
.(依据
垂直平分
.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点是否在线段
的垂直平分线上,请直接回答,不必证明;
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接,以
为一边在
的左下方作正方形
,发现点
在线段
的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接,以
为一边在
的右上方作正方形
,可以发现点
,点
都在线段
的垂直平分线上,除此之外,请观察矩形
和正方形
的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.

如图,在中,
,
,
,点
是
的中点,以
为直径作
,
分别与
,
交于点
,
,过点
作
的切线
,交
于点
,则
的长为 .

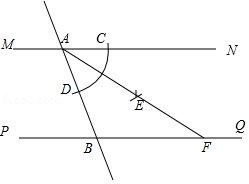
如图,直线,直线
分别与
,
相交于点
,
.小宇同学利用尺规按以下步骤作图:①以点
为圆心,以任意长为半径作弧交
于点
,交
于点
;②分别以
,
为圆心,以大于
长为半径作弧,两弧在
内交于点
;③作射线
交
于点
.若
,
,则线段
的长为 .
如图,在 中, , , ,将 绕点 按逆时针方向旋转得到△ ,此时点 恰好在 边上,则点 与点 之间的距离为

| A. |
12 |
B. |
6 |
C. |
|
D. |
|
综合与实践
背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名数学著作《周髀算经》中,为了方便,在本题中,我们把三边的比为的三角形称为
,4,
型三角形,例如:三边长分别为9,12,15或
,
,
的三角形就是
,4,
型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
实践操作 如图1,在矩形纸片中,
,
.
第一步:如图2,将图1中的矩形纸片沿过点
的直线折叠,使点
落在
上的点
处,折痕为
,再沿
折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点与点
重合,折痕为
,然后展平,隐去
.
第三步:如图4,将图3中的矩形纸片沿折叠,得到△
,再沿
折叠,折痕为
,
与折痕
交于点
,然后展平.

问题解决
(1)请在图2中证明四边形是正方形.
(2)请在图4中判断与
的数量关系,并加以证明;
(3)请在图4中证明,4,
型三角形;
探索发现
(4)在不添加字母的情况下,图4中还有哪些三角形是,4,
型三角形?请找出并直接写出它们的名称.
如图,内接于
,且
为
的直径,
,与
交于点
,与过点
的
的切线交于点
.
(1)若,
,求
的长.
(2)试判断与
的数量关系,并说明理由.

请阅读下列材料,并完成相应的任务:
阿基米德折弦定理
阿基米德 ,公元前 公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.
阿拉伯 年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据 译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1, 和 是 的两条弦(即折线 是圆的一条折弦), , 是 的中点,则从 向 所作垂线的垂足 是折弦 的中点,即 .下面是运用"截长法"证明 的部分证明过程.证明:如图2,在 上截取 ,连接 , , 和 .
是 的中点,
.
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知等边 内接于 , , 为 上一点, , 于点 ,则 的周长是 .
已知:如图,、
是
的两条弦,且
,
是
延长线上一点,联结
并延长交
于点
,联结
并延长交
于点
.
(1)求证:;
(2)如果,求证:四边形
是菱形.
