如图,菱形 的一边 在 轴的负半轴上, 是坐标原点, 点坐标为 ,对角线 和 相交于点 且 .若反比例函数 的图象经过点 ,并与 的延长线交于点 ,则 .

如图,反比例函数y= 与一次函数y=k2x+b的图象交于A(2,4),B(﹣4,m)两点.
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)若M(x1,y1),N(x2,y2)是反比例函数y= 的图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限.

如图,已知反比例函数 的图象与反比例函数 的图象关于 轴对称, , 是函数 图象上的两点,连接 ,点 是函数 图象上的一点,连接 , .
(1)求 , 的值;
(2)求 所在直线的表达式;
(3)求 的面积.

如图,在平面直角坐标系 xOy中,反比例函数 y= 的图象与一次函数 y= k( x﹣2)的图象交点为 A(3,2), B( x, y).
(1)求反比例函数与一次函数的解析式及 B点坐标;
(2)若 C是 y轴上的点,且满足△ ABC的面积为10,求 C点坐标.

设函数 , .
(1)当 时,函数 的最大值是 ,函数 的最小值是 ,求 和 的值.
(2)设 ,且 ,当 时, ;当 时, .圆圆说:“ 一定大于 ”.你认为圆圆的说法正确吗?为什么?
将直线  向下平移1个单位长度,得到直线
向下平移1个单位长度,得到直线  ,若反比例函数
的图象与直线
,若反比例函数
的图象与直线  相交于点
相交于点  ,且点
,且点  的纵坐标是3.
的纵坐标是3.
(1)求  和
和  的值;
的值;
(2)结合图象求不等式 的解集.
如图,在直角坐标系中, 的直角边 在 轴上, , ,反比例函数 的图象经过 边的中点 .
(1)求这个反比例函数的表达式;
(2)若 与 成中心对称,且 的边 在 轴的正半轴上,点 在这个函数的图象上.
①求 的长;
②连接 , ,证明四边形 是正方形.

如图,直线 与反比例函数 的图象交于 , 两点,已知点 的坐标为 , 的面积为8.
(1)填空:反比例函数的关系式为 ;
(2)求直线 的函数关系式;
(3)动点 在 轴上运动,当线段 与 之差最大时,求点 的坐标.

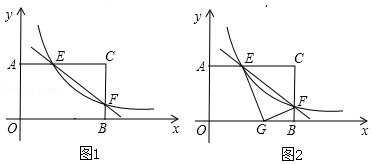
矩形 中, , .分别以 , 所在直线为 轴, 轴,建立如图1所示的平面直角坐标系. 是 边上一个动点(不与 , 重合),过点 的反比例函数 的图象与边 交于点 .
(1)当点 运动到边 的中点时,求点 的坐标;
(2)连接 ,求 的正切值;
(3)如图2,将 沿 折叠,点 恰好落在边 上的点 处,求此时反比例函数的解析式.
如图,一次函数 与反比例函数 的图象交于点 , .
(1)求反比例函数和一次函数的解析式;
(2)判断点 是否在一次函数 的图象上,并说明理由;
(3)写出不等式 的解集.

如图,正比例函数 与反比例函数 的图象交于点 ,过点 作 轴于点 , ,点 在线段 上,且 .
(1)求 的值及线段 的长;
(2)点 为 点上方 轴上一点,当 与 的面积相等时,请求出点 的坐标.

如图,在平面直角坐标系中,一次函数 和 的图象相交于点 ,反比例函数 的图象经过点 .
(1)求反比例函数的表达式;
(2)设一次函数 的图象与反比例函数 的图象的另一个交点为 ,连接 ,求 的面积.

如图,在平面直角坐标系中, 点的坐标为 , 轴于点 , ,反比例函数 的图象的一支分别交 、 于点 、 .延长 交反比例函数的图象的另一支于点 .已知点 的纵坐标为 .
(1)求反比例函数的解析式;
(2)求直线 的解析式;
(3)求 .

如图, 是反比例函数 在第一象限图象上一点,连接 ,过 作 轴,截取 在 右侧),连接 ,交反比例函数 的图象于点 .
(1)求反比例函数 的表达式;
(2)求点 的坐标;
(3)求 的面积.
